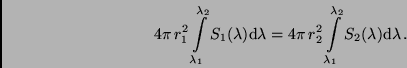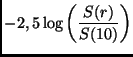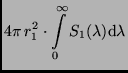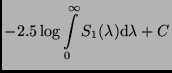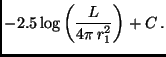Next: Die interstellare Extinktion und
Up: Grundlagen
Previous: Einführung
Contents
Informieren Sie sich zunächst in Aufgabe Nr. 8 über scheinbare
Helligkeiten und Farbenindizes.
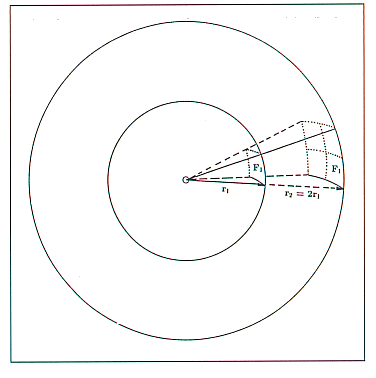
Denken wir uns in guter Näherung
zunächst den interstellaren Raum als frei von jeglicher Materie, so daß
dort keine Strahlung erzeugt oder vernichtet wird und betrachten die
Strahlung eines Sterns im Abstand 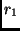 und
und
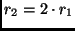 (siehe
Abb. 1). Seien weiter
(siehe
Abb. 1). Seien weiter 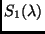 und
und 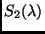 die in den beiden
Entfernungen beobachteten Strahlungsströme
die in den beiden
Entfernungen beobachteten Strahlungsströme
![${\rm [J\,s^{-1}m^{-2}nm^{-1}]}$](img1521.png) ,
so muß gelten:
,
so muß gelten:
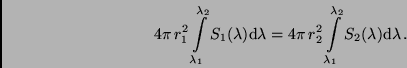 |
(1) |
Der Gesamtstrahlungsstrom durch die Kugeloberflächen mit den Radien
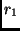 und
und 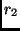 muß unter den von uns genannten Bedingungen gleich
sein.
Während die Gesamtstrahlung unabhängig
von der Entfernung ist, nimmt der beobachtete Strahlungsstrom mit dem
Quadrat der Entfernung ab. Dieser Effekt wird geometrische Verdünnung
der Strahlung genannt. Die Astronomen definierten deshalb neben der
scheinbaren Helligkeit die absolute Helligkeit eines Sterns als
entfernungsunabhängige Größe.
Die absolute Helligkeit
muß unter den von uns genannten Bedingungen gleich
sein.
Während die Gesamtstrahlung unabhängig
von der Entfernung ist, nimmt der beobachtete Strahlungsstrom mit dem
Quadrat der Entfernung ab. Dieser Effekt wird geometrische Verdünnung
der Strahlung genannt. Die Astronomen definierten deshalb neben der
scheinbaren Helligkeit die absolute Helligkeit eines Sterns als
entfernungsunabhängige Größe.
Die absolute Helligkeit 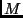 eines Sterns ist gleich der scheinbaren
Helligkeit
eines Sterns ist gleich der scheinbaren
Helligkeit 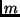 des Sterns, wenn sich dieser in einer Entfernung von 10 pc
befinden würde.
Für die
des Sterns, wenn sich dieser in einer Entfernung von 10 pc
befinden würde.
Für die 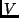 -Helligkeit des
-Helligkeit des 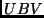 -Systems könnten wir mit dieser Definition
jetzt schreiben:
-Systems könnten wir mit dieser Definition
jetzt schreiben:
Die Differenz 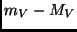 ist der Entfernungsmodul und
ist der Entfernungsmodul und 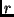 die
Entfernung des Sterns in Parsek. Die absolute Helligkeit eines Sterns
kann z.B. durch eine Spektralklassifikation des Sterns bestimmt werden.
In verschiedenen photometrischen Systemen kann man Spektraltyp und
absolute Helligkeit auch aus der Lage des Sterns in einem
Zwei-Farben-Diagramm ableiten.
Wie auch die scheinbare Helligkeit ist die absolute Helligkeit ein Maß
für den Strahlungsstrom in einem definierten Wellenlängenbereich.
Betrachtet man dagegen den Strahlungsstrom über den gesamten
Wellenlängenbereich, in dem ein Stern strahlt, gelangt man zur
bolometrischen Helligkeit. Der Wert der Gesamtstrahlung ist dann
gleich der Leuchtkraft
die
Entfernung des Sterns in Parsek. Die absolute Helligkeit eines Sterns
kann z.B. durch eine Spektralklassifikation des Sterns bestimmt werden.
In verschiedenen photometrischen Systemen kann man Spektraltyp und
absolute Helligkeit auch aus der Lage des Sterns in einem
Zwei-Farben-Diagramm ableiten.
Wie auch die scheinbare Helligkeit ist die absolute Helligkeit ein Maß
für den Strahlungsstrom in einem definierten Wellenlängenbereich.
Betrachtet man dagegen den Strahlungsstrom über den gesamten
Wellenlängenbereich, in dem ein Stern strahlt, gelangt man zur
bolometrischen Helligkeit. Der Wert der Gesamtstrahlung ist dann
gleich der Leuchtkraft
![$L\,{\rm [J\,s^{-1}]}$](img1530.png) des Sterns. Es gilt:
des Sterns. Es gilt:
Die absolute bolometrische Helligkeit 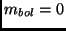 entspricht der
Leuchtkraft
entspricht der
Leuchtkraft
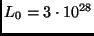 W.
Kennt man die Energieverteilung im Sternspektrum, kann man leicht die
Helligkeiten eines bestimmten Farbsystems in bolometrische Helligkeiten
umrechnen (siehe auch [5]). Die Differenz zwischen der
W.
Kennt man die Energieverteilung im Sternspektrum, kann man leicht die
Helligkeiten eines bestimmten Farbsystems in bolometrische Helligkeiten
umrechnen (siehe auch [5]). Die Differenz zwischen der 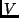 -Helligkeit
und der bolometrischen Helligkeit wird bolometrische Korrektion genannt:
-Helligkeit
und der bolometrischen Helligkeit wird bolometrische Korrektion genannt:
 |
(4) |
Normalerweise wird die bolometrische Korrektion für Sterne, die ihr
Strahlungsmaximum im visuellen Bereich haben, gleich Null gesetzt.
(Für einen schwarzen Strahler nimmt die bolometrische Korrektion bei einer
Temperatur von
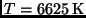 einen Minimalwert an.) Die obige
Konvention hat zur Folge, daß die Korrektur für alle Sterne negativ ist.
einen Minimalwert an.) Die obige
Konvention hat zur Folge, daß die Korrektur für alle Sterne negativ ist.




Next: Die interstellare Extinktion und
Up: Grundlagen
Previous: Einführung
Contents
Juergen Weiprecht
2002-10-29