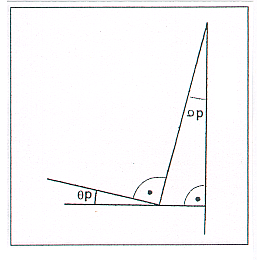
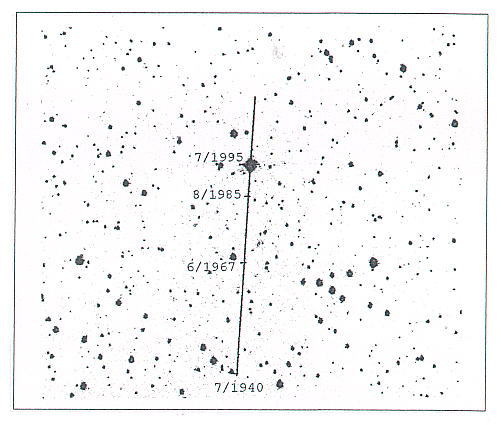
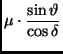Table 1:
Sterne mit Eigenbewegung 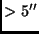 /a:
/a:
| Name |
Katalog- |
Stern- |
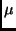 |
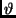 |
fotograf. |
Spektral- |
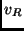 in in |
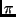 in in |
RA |
DEC |
| |
Nr. |
bild |
in |
in |
Helligkeit in |
klasse |
km/s |
 |
(1950) |
(1950) |
| |
|
|
 /a /a |
 |
m |
|
|
|
h m s |
 |
| Barnard`s Stern |
GL 699 |
Oph |
10,31 |
356 |
11,3 |
M5 |
-111 |
0,5453 |
17 55 23 |
 04 33,3 04 33,3 |
| Kapteyn's Stern |
GL 191 |
Pic |
8,71 |
131 |
10 |
M0 |
245,5 |
0,2583 |
05 09 41 |
 44 59,9 44 59,9 |
| Groombridge 1830 |
GL 451 |
UMa |
7,05 |
145 |
7 |
G5 |
-99,1 |
0,116 |
11 50 06 |
 38 04,7 38 04,7 |
| Lacaille 9352 |
GL 887 |
PsA |
6,9 |
79 |
8,6 |
M2 |
9,5 |
0,2843 |
23 02 39 |
 36 08,5 36 08,5 |
| Cordoba 32416 |
GL 1 |
Scl |
6,1 |
112 |
10 |
M3 |
22,9 |
0,2218 |
00 02 28 |
 37 36,2 37 36,2 |
| 61 Cyg A/B |
GL 820 |
Cyg |
5,22 |
52 |
6,2 / 7,2 |
K5 / K7 |
-64,8/-64,3 |
0,2887 |
21 04 40 |
 38 38,0 38 38,0 |
| Ross 619 |
GL 299 |
Cnc |
5,21 |
167 |
14,2 |
M6 |
-35 |
0,148 |
08 09 12 |
 08 59,6 08 59,6 |
Die Eigenbewegungen, Radialgeschwindigkeiten, Parallaxen und Positionen
wurden dem G
LIESE-Katalog
entnommen. Die restlichen Daten stammen aus B
URNHAM's Celestial Handbook
[
3].

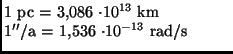 ,
,