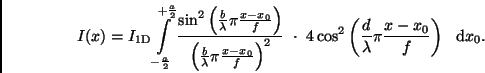Next: Zur auflösungsbegrenzenden Wirkung der
Up: Objekte der Sterninterferometrie
Previous: Doppelsterne
Contents
7.1.3.2 Gestirnsdurchmesser
Die bei der interferometrischen Vermessung von Doppelsternsystemen
vernachlässigte Winkelausdehnung der Sternscheibchen kann hinsichtlich
ihres Einflusses auf den Grad der Kohärenz (den Kontrast im
resultierenden Interferenzstreifensystem) des beim Beobachter
ankommenden Lichtes ermittelt werden.
Die nach einem Doppelspalt zu erwartende Intensitätsverteilung 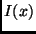 des
Lichtes einer ausgedehnten Quelle ergibt sich aus der inkohärenten
Überlagerung der Doppelspalt-Intensitätsverteilungen d
des
Lichtes einer ausgedehnten Quelle ergibt sich aus der inkohärenten
Überlagerung der Doppelspalt-Intensitätsverteilungen d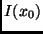 ,
die von allen
infinitesimal großen Raumwinkelbereichen der Quelle erzeugt und
durch Gleichung (1) beschrieben werden
(zwei Intensitätsverteilungen waren es beim Doppelstern).
Im folgenden sollen
,
die von allen
infinitesimal großen Raumwinkelbereichen der Quelle erzeugt und
durch Gleichung (1) beschrieben werden
(zwei Intensitätsverteilungen waren es beim Doppelstern).
Im folgenden sollen 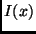 und darauf aufbauend
und darauf aufbauend 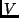 für eine in
für eine in
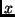 -Richtung ausgedehnte Spaltquelle mit einer über ihre Winkelausdehnung
-Richtung ausgedehnte Spaltquelle mit einer über ihre Winkelausdehnung
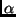 konstanten Intensität
konstanten Intensität 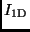 hergeleitet werden (
hergeleitet werden (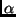 erscheint in der Brennebene als lineare Ausdehnung
erscheint in der Brennebene als lineare Ausdehnung 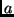 , siehe
Abb. 6). Entsprechend dem zuvor gesagten erhält man
, siehe
Abb. 6). Entsprechend dem zuvor gesagten erhält man 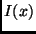 durch Integration der d
durch Integration der d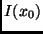 (beim Doppelstern hatte man einfach nur zu
addieren):
(beim Doppelstern hatte man einfach nur zu
addieren):
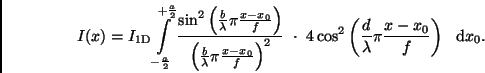 |
(6) |
Gleichung (6) kann analog zu Gleichung (3)
vereinfacht
werden, indem der modulierende Einfluß des Terms
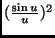 vernachlässigt wird, was im Falle einer gegen den Spaltabstand
vernachlässigt wird, was im Falle einer gegen den Spaltabstand 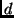 sehr
kleinen Spaltbreite im Zentrum der Intensitätsverteilung recht gut gilt.
Bei Verwendung der Hilfsgröße
sehr
kleinen Spaltbreite im Zentrum der Intensitätsverteilung recht gut gilt.
Bei Verwendung der Hilfsgröße
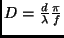 ergibt sich:
ergibt sich:
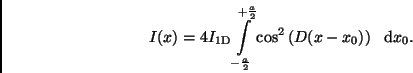 |
(7) |
Nach Anwendung verschiedener Winkelfunktionsbeziehungen und Integration
erhält man:
woraus sich 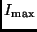 ,
, 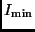 und daraus folgend
und daraus folgend 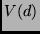 ergeben:
ergeben:
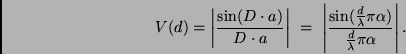 |
(8) |
Der mit (8) erhaltene Verlauf von 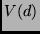 ist in
Abb. 7 dargestellt.
Die Abb. zeigt außerdem zwei weitere Kontrastfunktionen
ist in
Abb. 7 dargestellt.
Die Abb. zeigt außerdem zwei weitere Kontrastfunktionen 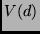 , die
im Falle anderer 1D-Intensitätsverteilungen des Objektes zu
erwarten sind, wobei auf deren Herleitung, die prinzipiell im Sinne der
zuvor beschriebenen verläuft, auf Grund des erhöhten Rechenaufwandes
verzichtet wird. Bei Betrachtung der in Abb. 7
gezeigten
Intensitätsverteilungen und der dazugehörigen Kontrastfunktionen
zeigt sich eine Ähnlichkeit zwischen den Ausdrücken für
, die
im Falle anderer 1D-Intensitätsverteilungen des Objektes zu
erwarten sind, wobei auf deren Herleitung, die prinzipiell im Sinne der
zuvor beschriebenen verläuft, auf Grund des erhöhten Rechenaufwandes
verzichtet wird. Bei Betrachtung der in Abb. 7
gezeigten
Intensitätsverteilungen und der dazugehörigen Kontrastfunktionen
zeigt sich eine Ähnlichkeit zwischen den Ausdrücken für 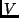 und
den entsprechenden Beugungsmustern für Blendenöffnungen gleichen
Aussehens, die ihren Ausdruck im van Cittert-Zernike-Theorem findet.
Das van CITTERT-ZERNIKE-Theorem besagt, daß der Kohärenzgrad der
Strahlung eines Objektes, der
von einem Punkt P
und
den entsprechenden Beugungsmustern für Blendenöffnungen gleichen
Aussehens, die ihren Ausdruck im van Cittert-Zernike-Theorem findet.
Das van CITTERT-ZERNIKE-Theorem besagt, daß der Kohärenzgrad der
Strahlung eines Objektes, der
von einem Punkt P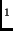 bezüglich eines Punktes P
bezüglich eines Punktes P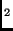 im Wellenfeld
(die Korrelation der Wellenbewegung in diesen Punkten) beim Beobachter
entstanden ist, dem bei P
im Wellenfeld
(die Korrelation der Wellenbewegung in diesen Punkten) beim Beobachter
entstanden ist, dem bei P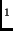 vorliegenden Wert der bezüglich P
vorliegenden Wert der bezüglich P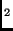 auf eins normierten Verteilung der dem Objekt entsprechenden
Beugungsintensität entspricht.
Sind die Punkte P
auf eins normierten Verteilung der dem Objekt entsprechenden
Beugungsintensität entspricht.
Sind die Punkte P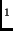 und P
und P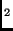 nicht weit voneinander entfernt
(bei einer kleinen Winkelausdehnung des Objektes), d.h. im Falle
FRAUNHOFERscher Beugung, entspricht der Kohärenzgrad (und damit der
Kontrast) der normalisierten FOURIERtransformierten der
Intensitätsverteilung des Objektes. Bei einer über das Objekt
konstanten Intensität ist
nicht weit voneinander entfernt
(bei einer kleinen Winkelausdehnung des Objektes), d.h. im Falle
FRAUNHOFERscher Beugung, entspricht der Kohärenzgrad (und damit der
Kontrast) der normalisierten FOURIERtransformierten der
Intensitätsverteilung des Objektes. Bei einer über das Objekt
konstanten Intensität ist 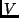 im Falle einer Spaltquelle also die
im Falle einer Spaltquelle also die
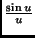 -Funktion und im Falle einer kreisförmigen Quelle die
BESSELfunktion 1. Ordnung.
Der für eine kreisförmige Scheibe konstanter
Intensität gültige Verlauf von
-Funktion und im Falle einer kreisförmigen Quelle die
BESSELfunktion 1. Ordnung.
Der für eine kreisförmige Scheibe konstanter
Intensität gültige Verlauf von 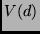 ist derjenige, der
zur Bestimmung der Winkeldurchmesser
ist derjenige, der
zur Bestimmung der Winkeldurchmesser 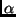 von Himmelskörpern
in erster Näherung genügt:
von Himmelskörpern
in erster Näherung genügt:
 |
(9) |
Bei 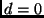 ist
ist 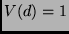 , bei
, bei
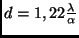 ,
(
,
(
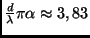 ) wird
) wird 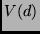 erstmals Null.
Mit der weiteren Vergrößerung von
erstmals Null.
Mit der weiteren Vergrößerung von 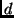 wächst
wächst 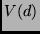 wieder,
wobei im Zentrum des Interferenzstreifensystems diesmal ein Minimum zu
finden ist. Bei
wieder,
wobei im Zentrum des Interferenzstreifensystems diesmal ein Minimum zu
finden ist. Bei
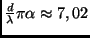 wird
wird 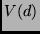 erneut zu Null. In dem folgenden Abschnitt von
erneut zu Null. In dem folgenden Abschnitt von 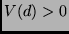 liegt im
Zentrum des Streifensystems wieder das Maximum usw..
Die in Abb. 8 gezeigten Verläufe von
liegt im
Zentrum des Streifensystems wieder das Maximum usw..
Die in Abb. 8 gezeigten Verläufe von 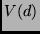 wurden
mit Hilfe Computerprogramms VISIBILITY [16] berechnet.
wurden
mit Hilfe Computerprogramms VISIBILITY [16] berechnet.




Next: Zur auflösungsbegrenzenden Wirkung der
Up: Objekte der Sterninterferometrie
Previous: Doppelsterne
Contents
Juergen Weiprecht
2002-10-29