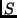 |
Solarkonstante, |
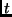 |
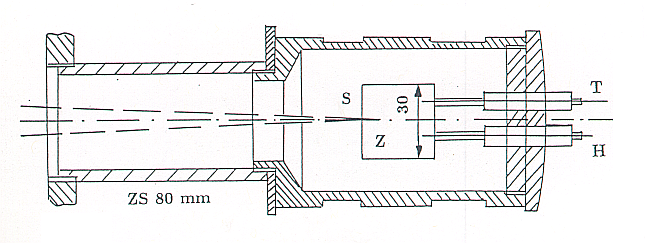
Zeitdauer der Einstrahlung auf den Zylinder, |
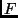 |
lichtsammelnde Fläche des Objektivs |
| |
(Durchmesser des Telementorobjektivs: 63 mm, |
| |
Durchmesser des Leitrohrobjektivs: 108 mm), |
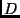 |
mittlere spektrale Durchlässigkeit der Optik |
| |
(Telementorobjektiv: 0,95, |
| |
Leitrohrobjektiv: 0,87), |
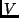 |
Wärmeverluste, |
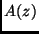 |
spektrale Durchlässigkeit der Atmosphäre bei der Zenitdistanz 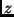 , , |
| |
|
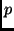 |
Transmission der Atmosphäre im visuellen Spektralbereich bei 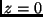 : : |
| |
| klarer Himmel: |
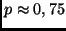 ; ; |
Absorption 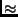 0,3 mag; 0,3 mag; |
| dunstiger Himmel: |
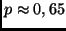 ; ; |
Absorption 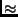 0,5 mag; 0,5 mag; |
| leichte Cirruswolken: |
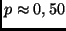 ; ; |
Absorption 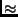 0,75 mag; 0,75 mag; |
| stärkere Cirruswolken: |
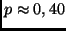 ; ; |
Absorption 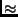 1 mag; 1 mag; |
|
| |
|
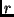 |
Entfernung Erde-Sonne, |
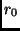 |
mittlere Entfernung Erde-Sonne, |
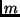 |
Masse des Aluminiumzylinders = 100 g, |
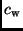 |
spezifische Wärmekapazität von Al 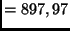 J kg J kg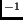 K K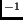 . . |