Next: Seeing, Szintillation, Refraktion und
Up: Die Einflüsse der Erdatmosphäre
Previous: Die Einflüsse der Erdatmosphäre
Contents
Die Durchlässigkeit der Erdatmosphäre für elektromagnetische Strahlung
ist stark wellenlängenabhängig, wobei die Abschwächung der Strahlung
durch Absorption und Streuung erfolgt. Durch die Extinktion
gelangen im visuellen Spektralbereich etwa nur 5/6 der einfallenden Strahlung
bis zur Erdoberfläche.
Bei dem Prozeß der Absorption wird ein Photon
vernichtet und dessen Energie geht auf das absorbierende Molekül über,
das dadurch in einen angeregten Energiezustand gelangt.
Ursache für die Absorption im Ultraviolettbereich (UV) sind die Atome und
Moleküle N, 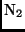 , O,
, O, 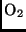 und
und 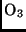 . Im
Infrarotbereich (IR) hingegen absorbieren vor allem
. Im
Infrarotbereich (IR) hingegen absorbieren vor allem 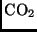 und
und
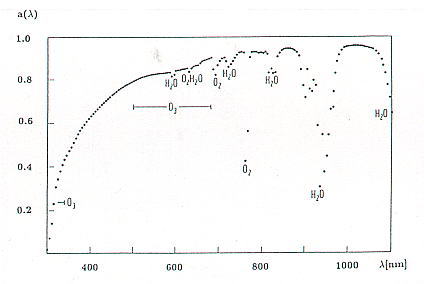
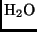 (siehe Abb. 4 und Abb. 1 in Aufgabe 4). Diese
Atmosphärenbestandteile bewirken,
daß im UV eine völlige Undurchlässigkeit bei Wellenlängen kleiner als
290 nm herrscht. Im IR und im Radiobereich gelangt dagegen in einigen
schmalen Gebieten - sogenannten Fenstern - noch Strahlung bis zur
Erdoberfläche.
Streuung beinhaltet die Kollision eines Photons mit einem Teilchen
und die anschließende Richtungsänderung des Photons. Es ändert sich
sowohl der energetische Zustand des Photons als auch der des Teilchens.
Die Streuung in der Erdatmosphäre wird durch Teilchen sehr unterschiedlicher
Größe verursacht. Die Streuung an Luftmolekülen mit Größen von
(siehe Abb. 4 und Abb. 1 in Aufgabe 4). Diese
Atmosphärenbestandteile bewirken,
daß im UV eine völlige Undurchlässigkeit bei Wellenlängen kleiner als
290 nm herrscht. Im IR und im Radiobereich gelangt dagegen in einigen
schmalen Gebieten - sogenannten Fenstern - noch Strahlung bis zur
Erdoberfläche.
Streuung beinhaltet die Kollision eines Photons mit einem Teilchen
und die anschließende Richtungsänderung des Photons. Es ändert sich
sowohl der energetische Zustand des Photons als auch der des Teilchens.
Die Streuung in der Erdatmosphäre wird durch Teilchen sehr unterschiedlicher
Größe verursacht. Die Streuung an Luftmolekülen mit Größen von
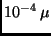 m wird als Rayleigh-Streuung bezeichnet und der
Streu- oder Extinktionskoeffizient
m wird als Rayleigh-Streuung bezeichnet und der
Streu- oder Extinktionskoeffizient
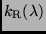 in Größenklassen ist
proportional zu
in Größenklassen ist
proportional zu 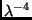 . Für Aerosole mit Teilchengrößen
zwischen
. Für Aerosole mit Teilchengrößen
zwischen
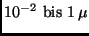 m ist die Wellenlängenabhängigkeit
durch
m ist die Wellenlängenabhängigkeit
durch
![\begin{displaymath}
k_{\rm D}(\lambda) = {-2.5 \lg e^{-\beta \lambda^{-\alpha}} }
\; ; \;
[\lambda/\mu {\rm m}]
\end{displaymath}](img808.png) |
(11) |
gegeben [6]. Sehr große Teilchen mit Durchmessern zwischen
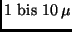 m streuen unabhängig von der Wellenlänge und
teilweise in die Richtung zurück, aus der das Licht ursprünglich kam.
Ein Effekt, der sich gut bei Nebel beobachten läßt. Die blaue Färbung
des Tageshimmels rührt von der Rayleigh-Streuung her.
Der beobachtete Gesamtextinktionskoeffizient
m streuen unabhängig von der Wellenlänge und
teilweise in die Richtung zurück, aus der das Licht ursprünglich kam.
Ein Effekt, der sich gut bei Nebel beobachten läßt. Die blaue Färbung
des Tageshimmels rührt von der Rayleigh-Streuung her.
Der beobachtete Gesamtextinktionskoeffizient 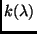 setzt sich
additiv aus den einzelnen Teilkomponenten zusammen. Beobachtet man im
visuellen Spektralbereich und nicht
gerade in einer speziellen Absorptionslinie (siehe Abb. 4), so kann man
schreiben:
setzt sich
additiv aus den einzelnen Teilkomponenten zusammen. Beobachtet man im
visuellen Spektralbereich und nicht
gerade in einer speziellen Absorptionslinie (siehe Abb. 4), so kann man
schreiben:
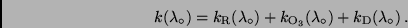 |
(12) |
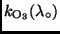 ist der Beitrag der Absorption durch
Ozon zum Gesamtextinktionskoeffizienten. Die Größe der einzelnen
Teilbeiträge hängt vom verwendeten Atmosphärenmodell ab. In Tabelle 1
sind die Extinktionskoeffizienten für die einzelnen Farbbereiche für
ein Standardmodell gegeben. Die Wellenlängenabhängigkeit der einzelnen
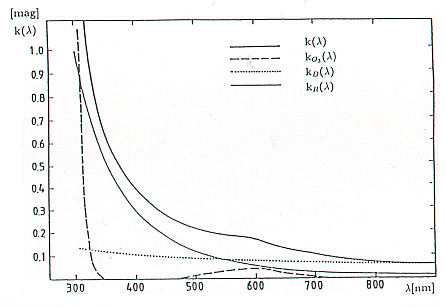
Extinktionsbeiträge ist in Abb. 5 dargestellt.
Der Anteil der Aerosolextinktion schwankt zeitlich
und räumlich sehr stark und kann nur durch Beobachtung bestimmt werden.
Die Rayleigh-Streuung ist abhängig vom Luftdruck und kann mit der
folgenden Formel für den Luftdruck am Beobachtungsort korrigiert werden:
ist der Beitrag der Absorption durch
Ozon zum Gesamtextinktionskoeffizienten. Die Größe der einzelnen
Teilbeiträge hängt vom verwendeten Atmosphärenmodell ab. In Tabelle 1
sind die Extinktionskoeffizienten für die einzelnen Farbbereiche für
ein Standardmodell gegeben. Die Wellenlängenabhängigkeit der einzelnen
Extinktionsbeiträge ist in Abb. 5 dargestellt.
Der Anteil der Aerosolextinktion schwankt zeitlich
und räumlich sehr stark und kann nur durch Beobachtung bestimmt werden.
Die Rayleigh-Streuung ist abhängig vom Luftdruck und kann mit der
folgenden Formel für den Luftdruck am Beobachtungsort korrigiert werden:
 |
(13) |
Mit 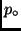 ist der Normalluftdruck (101,325 kPa) und mit
ist der Normalluftdruck (101,325 kPa) und mit 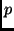 der Luftdruck
am Beobachtungsort bezeichnet.
Die Beobachtungen zeigen, daß sich die atmosphärische Transmission in
Abhängigkeit von
der Luftdruck
am Beobachtungsort bezeichnet.
Die Beobachtungen zeigen, daß sich die atmosphärische Transmission in
Abhängigkeit von 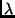 und der Zenitdistanz
und der Zenitdistanz 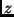 in der Form
in der Form
 |
(14) |
darstellen läßt. Dabei ist
![$\kappa(\lambda) \ [{\rm m^{-1}}]$](img816.png) der
Extinktionskoeffizient pro Längeneinheit und
der
Extinktionskoeffizient pro Längeneinheit und 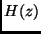 eine charakteristische
Länge, die die vom Lichtstrahl durchquerte optische Weglänge bezeichnet.
eine charakteristische
Länge, die die vom Lichtstrahl durchquerte optische Weglänge bezeichnet.
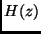 ist dabei gleich der Höhe einer Luftsäule konstanter Dichte,
die die gleiche Luftmasse enthält, wie die vom Sternlicht tatsächlich
durchlaufene Luftsäule. Unter Normalbedingungen, für einen Beobachter
auf Meeresniveau, ergibt sich in Zenitrichtung
ist dabei gleich der Höhe einer Luftsäule konstanter Dichte,
die die gleiche Luftmasse enthält, wie die vom Sternlicht tatsächlich
durchlaufene Luftsäule. Unter Normalbedingungen, für einen Beobachter
auf Meeresniveau, ergibt sich in Zenitrichtung
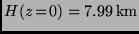 als Äquivalenthöhe der Atmosphäre (Höhe einer homogenen Atmosphäre konstanter
Dichte). Für die Bestimmung der Extinktionskorrektur von Sternen bei
einer vorgegebenen Zenitdistanz ist es nun wichtig zu wissen, um wieviel
länger der zurückgelegte Weg des Lichtstrahls
als Äquivalenthöhe der Atmosphäre (Höhe einer homogenen Atmosphäre konstanter
Dichte). Für die Bestimmung der Extinktionskorrektur von Sternen bei
einer vorgegebenen Zenitdistanz ist es nun wichtig zu wissen, um wieviel
länger der zurückgelegte Weg des Lichtstrahls 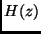 ist, als der bei einer
Beobachtung im Zenit mit
ist, als der bei einer
Beobachtung im Zenit mit 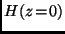 . Die Astronomen bezeichnen nun die
dimensionslose Größe
. Die Astronomen bezeichnen nun die
dimensionslose Größe 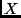
 |
(15) |
die das Verhältnis der optischen Weglängen darstellt, als Luftmasse.
Ersetzt man nun in Gleichung (14) 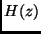 aus Gleichung (15) und die
Transmission durch das Verhältnis des beobachteten Strahlungsstromes
aus Gleichung (15) und die
Transmission durch das Verhältnis des beobachteten Strahlungsstromes
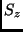 mit dem an der Obergrenze der Atmosphäre eintretenden
Strahlungsstrom
mit dem an der Obergrenze der Atmosphäre eintretenden
Strahlungsstrom 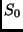 , erhält man:
, erhält man:
 |
(16) |
Beim Übergang zu den Helligkeiten ergibt sich:
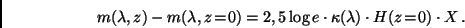 |
(17) |
Stellt man die Gleichung nach
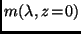 um und ersetzt die rechte
Seite mit Ausnahme der Luftmasse durch den Extinktionskoeffizienten
um und ersetzt die rechte
Seite mit Ausnahme der Luftmasse durch den Extinktionskoeffizienten
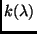 , ausgedrückt in Größenklassen [mag], so erhält man:
, ausgedrückt in Größenklassen [mag], so erhält man:
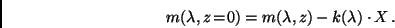 |
(18) |
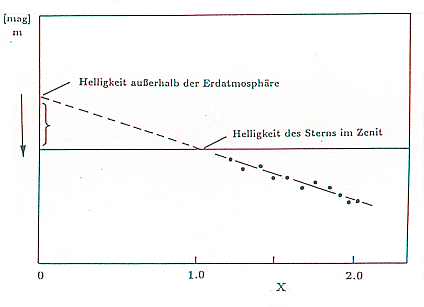
Die Helligkeit eines Sterns nimmt also bei genügend schmaler Bandbreite
des photometrischen Systems, aufgetragen über der Luftmasse, linear ab
(siehe Abb. 6).
Die Extinktion erhält man praktisch durch die Beobachtung von Standardsternen
im jeweiligen photometrischen System. Für einen beliebigen
Standardstern der Helligkeit 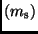 , beobachtet mit einem vorgegebenen
Instrument
, beobachtet mit einem vorgegebenen
Instrument 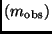 , kann man nach Gleichung (18) schreiben:
, kann man nach Gleichung (18) schreiben:
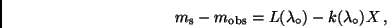 |
(19) |
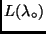 ist ein instrumenteller Nullpunkt, der durch die
Quanteneffektivität des Empfängers sowie die Transmission von Teleskop,
Filter und Atmosphäre bei
ist ein instrumenteller Nullpunkt, der durch die
Quanteneffektivität des Empfängers sowie die Transmission von Teleskop,
Filter und Atmosphäre bei 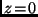 bestimmt wird.
Die Luftmasse
bestimmt wird.
Die Luftmasse 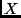 ergibt sich für eine planparallele homogene Atmosphäre
konstanter Dichte gerade zu
ergibt sich für eine planparallele homogene Atmosphäre
konstanter Dichte gerade zu 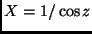 [5].
Für ein Kugelschalenmodel (siehe auch Aufgabe 2) ergibt sich:
[5].
Für ein Kugelschalenmodel (siehe auch Aufgabe 2) ergibt sich:
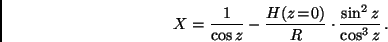 |
(20) |
Dabei ist 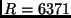 km der Erdradius.
Die Extinktion ist in verschiedenen Zeitskalen (Minuten, Stunden,
tages- und jahreszeitlich) veränderlich. Die kurzzeitigen Änderungen
stellen eine zusätzliche Rauschquelle bei der Beobachtung dar.
Sie können in den Farbenindizes durch die Benutzung eines
Mehrkanalphotometers oder quasigleichzeitige Messungen mit einem rotierenden
Filterrad erheblich reduziert werden.
Änderungen im Verlauf einer Nacht müssen bei der Reduktion entsprechend
berücksichtigt werden. Nimmt man an, daß die nächtliche Änderung der
Extinktion langsam und isotrop erfolgt, kann man zu Gleichung (19) einen
linearen Zeitterm hinzufügen [7].
km der Erdradius.
Die Extinktion ist in verschiedenen Zeitskalen (Minuten, Stunden,
tages- und jahreszeitlich) veränderlich. Die kurzzeitigen Änderungen
stellen eine zusätzliche Rauschquelle bei der Beobachtung dar.
Sie können in den Farbenindizes durch die Benutzung eines
Mehrkanalphotometers oder quasigleichzeitige Messungen mit einem rotierenden
Filterrad erheblich reduziert werden.
Änderungen im Verlauf einer Nacht müssen bei der Reduktion entsprechend
berücksichtigt werden. Nimmt man an, daß die nächtliche Änderung der
Extinktion langsam und isotrop erfolgt, kann man zu Gleichung (19) einen
linearen Zeitterm hinzufügen [7].
![\begin{displaymath}
m_{\rm s} - m_{\rm obs} = {L(\lambda _{\circ})
- k(\lambda _{\circ})X
+ D(\lambda _{\circ})t} \, ; {\rm [D, mag/h]}
\end{displaymath}](img837.png) |
(21) |
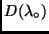 wird als Driftkoeffizient bezeichnet und in
Größenklassen pro Stunde gemessen. Er kann je nach meteorologischen
Bedingungen 0,001 bis 0,100 mag/h betragen.
wird als Driftkoeffizient bezeichnet und in
Größenklassen pro Stunde gemessen. Er kann je nach meteorologischen
Bedingungen 0,001 bis 0,100 mag/h betragen.




Next: Seeing, Szintillation, Refraktion und
Up: Die Einflüsse der Erdatmosphäre
Previous: Die Einflüsse der Erdatmosphäre
Contents
Juergen Weiprecht
2002-10-29