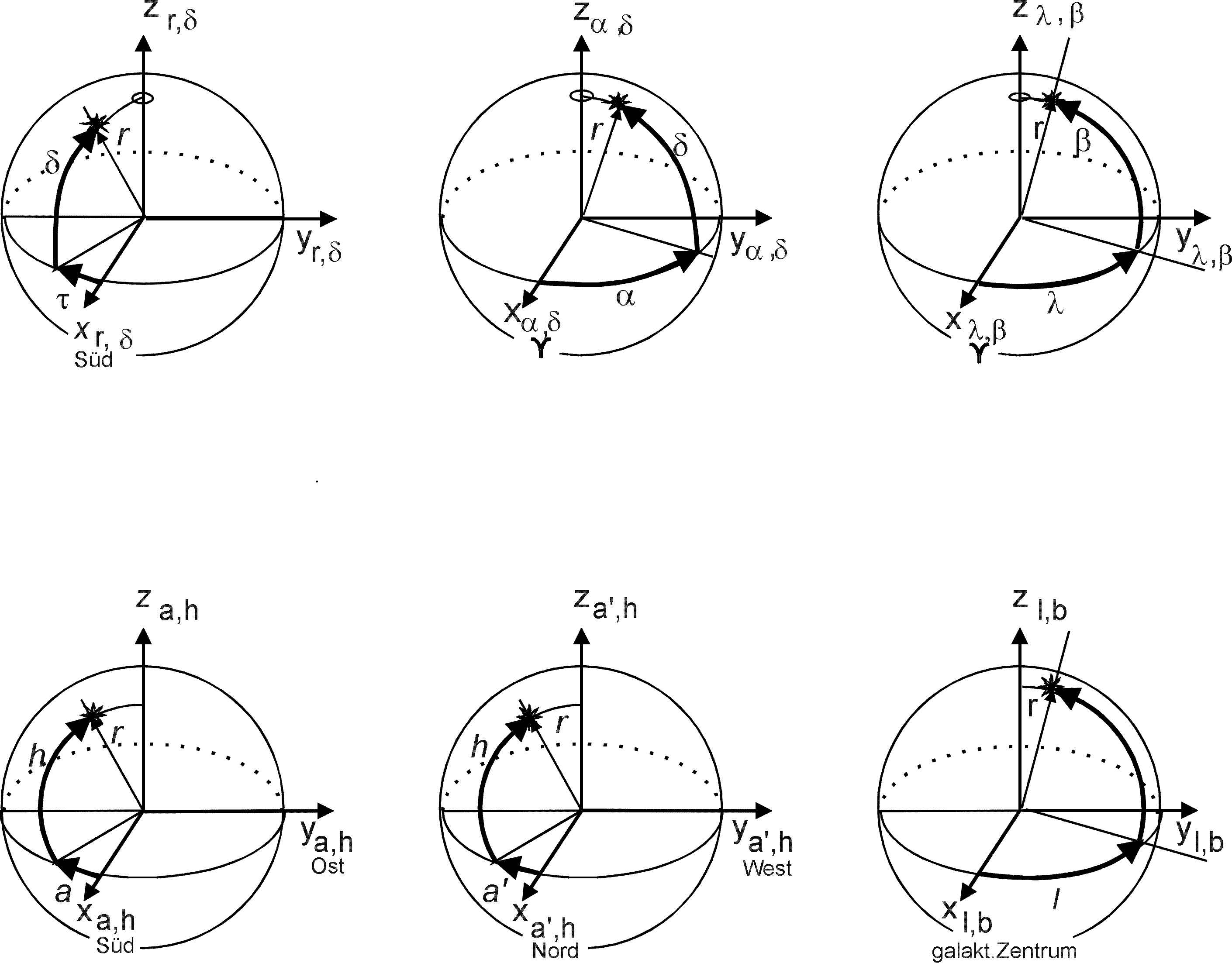
 |
| Abb. 3: Lage des kartesischen Koordinatensystems x,y,z in Bezug auf die verschiedenen astronomischen Koordinatensysteme. |
Die Herleitung der Transformationsgleichungen läuft in drei Schritten ab.
Zunächst werden die gegebenen sphärischen Koordinaten in kartesische
umgerechnet. Danach erfolgt die Drehung des kartesischen Dreibeins in die
Lage, die dem sphärischen System mit den gesuchten Koordinaten entspricht
(die Position des Ursprungs bleibt unverändert).
Die Koordinatentransformation wird durch eine Drehmatrix beschrieben.
Abschließend werden die "`neuen"' kartesischen Koordinaten in die
gesuchten sphärischen Koordinaten umgerechnet.
Die Koordinaten von beliebig zueinander verdrehten Dreibeinen werden
mittels einer
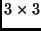
-Drehmatrix
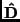
transformiert, deren
Elemente durch die 9 Richtungskosinus gebildet werden.
Die im zweiten Schritt der Herleitung benötigten Drehmatrizen
werden auf Grundlage spezieller Drehmatrizen
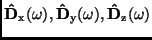
,
die jeweils nur die Drehung um die eine indizierte Achse
(Drehwinkel
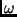
) ausführen, durch Matrizenmultiplikation erzeugt
(die Matrix mit der ersten Drehung steht dabei ganz rechts, siehe
Abb.
4). Die Drehwinkel werden entsprechend der bereits genannten
Konvention gemessen.
Die Anwendung der Drehmatrizen ist in Abb.
4 dargestellt.
Nach Einsetzen der in Abb.
3 gegebenen Umrechnungsbeziehungen
in die in Abb.
4 aufgelisteten Formeln ergeben sich z.B.
für die Transformation der Koordinaten des ruhenden
Äquatorsystems in diejenigen des astronomischen Horizontsystems
die folgenden Transformationsbeziehungen:
1cm

Abb. 1:
Zur Herleitung der Transformationsbeziehungen zwischen verschiedenen
astronomischen Koordinatensystemen.
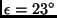
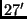 - Neigungswinkel zwischen Äquator- und Ekliptikebene,
- Neigungswinkel zwischen Äquator- und Ekliptikebene, 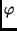 -
geographische Breite.
-
geographische Breite.



 Next: Optische Eigenschaften von Fernrohren
Up: Astronomische Koordinatensysteme
Previous: Galaktisches System
Contents
Juergen Weiprecht
2002-10-29
Next: Optische Eigenschaften von Fernrohren
Up: Astronomische Koordinatensysteme
Previous: Galaktisches System
Contents
Juergen Weiprecht
2002-10-29

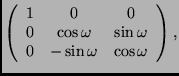


![]()
![]() - Neigungswinkel zwischen Äquator- und Ekliptikebene,
- Neigungswinkel zwischen Äquator- und Ekliptikebene, ![]() -
geographische Breite.
-
geographische Breite.