Next: Versuchsanleitung
Up: Bestimmung der Rotationsdauer der
Previous: Bestimmung der persönlichen Fleckenrelativzahl
Contents
Die Sonne rotiert differentiell (siehe [5]), wobei sich Unterschiede in der
Rotationsperiode besonders zwischen den mit einem starken Magnetfeld
verbundenen Sonnenphänomenen, z.B. Flecken und dem "`unmagnetischen"'
Photosphärengas ergeben. Da einzelne Flecken, vor allem in den ersten
Entwicklungsstadien einer Fleckengruppe, ihre heliographische Länge
verändern können, ergibt sich der genaue Wert der mittleren siderischen
Rotation der Sonne erst auf Grund längerer Beobachtungsreihen.
Bestimmt man für einen Fleck seinen Abstand 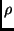 (im gleichen Maß wie
(im gleichen Maß wie
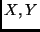 und
und 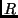 ) vom Mittelpunkt
) vom Mittelpunkt
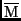 der sichtbaren Sonnenscheibe
(Abb. 1) und den in
der sichtbaren Sonnenscheibe
(Abb. 1) und den in
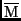 gemessenen Winkelabstand
gemessenen Winkelabstand 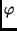 des
Flecks von der projizierten Rotationsachse, so ergibt sich für den auf den
Sonnenmittelpunkt S bezogenen Winkel
des
Flecks von der projizierten Rotationsachse, so ergibt sich für den auf den
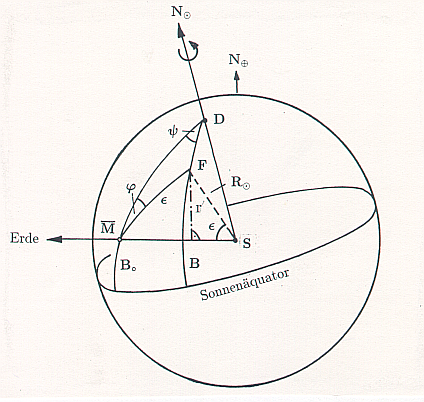
Sonnenmittelpunkt S bezogenen Winkel 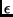 (Abb. 4)
(Abb. 4)
 |
(9) |
Der am Durchstoßpunkt D der Rotationsachse der Sonne durch die
Sonnenoberfläche auftretende Winkel 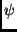 des Flecks vom
Zentralmeridian der Sonne läßt sich mit Hilfe des sphärischen Dreiecks
DF
des Flecks vom
Zentralmeridian der Sonne läßt sich mit Hilfe des sphärischen Dreiecks
DF
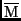 unter Anwendung des sphärischen
Sinussatzes (Abb. 4) errechnen:
unter Anwendung des sphärischen
Sinussatzes (Abb. 4) errechnen:
also
 |
(10) |
Die noch unbekannte heliographische Breite 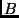 des Flecks ergibt sich mit
Hilfe des Seitenkosinussatzes zu
des Flecks ergibt sich mit
Hilfe des Seitenkosinussatzes zu
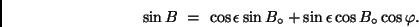 |
(11) |
Bestimmt man 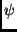 zu zwei verschiedenen Zeitpunkten
zu zwei verschiedenen Zeitpunkten 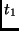 und
und 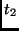 ,
,
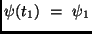 ,
,
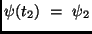 ,
,
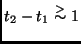 Tag, dann ergibt sich für die scheinbare Bewegung des
Sonnenflecks in bezug auf den Zentralmeridian
Tag, dann ergibt sich für die scheinbare Bewegung des
Sonnenflecks in bezug auf den Zentralmeridian
 |
(12) |
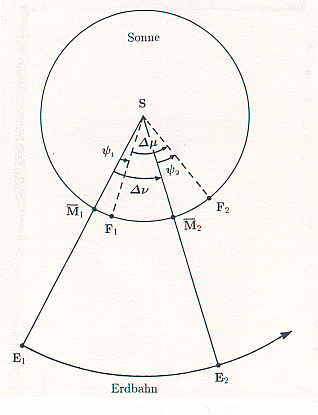
Bezeichnet 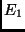 in Abb. 5 den Ort der Erde in ihrer Bahn um die Sonne zum
Zeitpunkt
in Abb. 5 den Ort der Erde in ihrer Bahn um die Sonne zum
Zeitpunkt 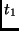 und
und 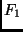 einen Punkt mit dem Winkelabstand
einen Punkt mit dem Winkelabstand 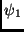 vom
Zentralmeridian zum Zeitpunkt
vom
Zentralmeridian zum Zeitpunkt 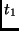 , so bewegt sich im Intervall
, so bewegt sich im Intervall
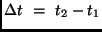 die Erde um den Winkel
die Erde um den Winkel 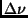 bis
bis 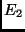 ,
der Punkt
,
der Punkt 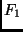 auf Grund der Sonnenrotation um den Winkel
auf Grund der Sonnenrotation um den Winkel 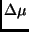 bis
bis
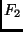 , wobei er dann den Winkelabstand
, wobei er dann den Winkelabstand 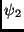 vom Zentralmeridian hat.
Nach Abb. 5 ist
vom Zentralmeridian hat.
Nach Abb. 5 ist
also
 |
(13) |
Bezeichnet man weiter mit
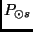 : die synodische Rotationsperiode der Sonne,
: die synodische Rotationsperiode der Sonne,
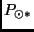 : die siderische Rotationsperiode der Sonne,
: die siderische Rotationsperiode der Sonne,
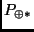 : die siderische Umlaufperiode der Erde um
die Sonne,
: die siderische Umlaufperiode der Erde um
die Sonne,
so gilt allgemein
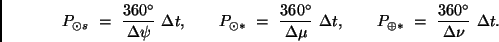 |
(14) |
Durch Einsetzen der Beziehung (13) erhält man die gesuchte siderische
Rotationsperiode der Sonne
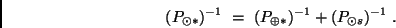 |
(15) |




Next: Versuchsanleitung
Up: Bestimmung der Rotationsdauer der
Previous: Bestimmung der persönlichen Fleckenrelativzahl
Contents
Juergen Weiprecht
2002-10-29

: die synodische Rotationsperiode der Sonne,
: die siderische Rotationsperiode der Sonne,
: die siderische Umlaufperiode der Erde um die Sonne,