



Next: Physikalische und geometrische Eigenschaften
Up: Grundlagen
Previous: Grundlagen
Contents
Die Bewegung zweier Massenpunkte um den gemeinsamen Schwerpunkt wird
durch eine vektorielle Differentialgleichung 2. Ordnung beschrieben,
die im Falle einer Bewegung um die Sonne lautet:
 |
(1) |
Hierin sind 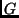 die Gravitationskonstante und
die Gravitationskonstante und 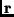 der
heliozentrische Ortsvektor des Objekts. Der Schwerpunkt des Systems
ist im Sonnenmittelpunkt gedacht, und die Masse des Objekts wurde
gegenüber der Sonnenmasse
der
heliozentrische Ortsvektor des Objekts. Der Schwerpunkt des Systems
ist im Sonnenmittelpunkt gedacht, und die Masse des Objekts wurde
gegenüber der Sonnenmasse 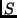 vernachlässigt. Die vollständige
Integration dieser Gleichung liefert sechs unabhängige Konstanten,
mit deren Hilfe es möglich ist, in einem
beliebig gewählten räumlichen Koordinatensystem den Ort des einen
Körpers bezüglich des anderen als Funktion der Zeit, also dessen
Bahnkurve, zu berechnen. Da die Bahn in jedem Falle einen Kegelschnitt
darstellt, sind in der Astronomie die folgenden sechs Größen
(Bahnelemente) zur Beschreibung der Bahn eines Himmelskörpers üblich
(vgl. Abb. 1):
vernachlässigt. Die vollständige
Integration dieser Gleichung liefert sechs unabhängige Konstanten,
mit deren Hilfe es möglich ist, in einem
beliebig gewählten räumlichen Koordinatensystem den Ort des einen
Körpers bezüglich des anderen als Funktion der Zeit, also dessen
Bahnkurve, zu berechnen. Da die Bahn in jedem Falle einen Kegelschnitt
darstellt, sind in der Astronomie die folgenden sechs Größen
(Bahnelemente) zur Beschreibung der Bahn eines Himmelskörpers üblich
(vgl. Abb. 1):
- Länge des aufsteigenden Knotens (
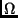 ): Sie ist der Winkel
in der Ebene der Ekliptik zwischen der Richtung zum Frühlingspunkt
und der Richtung zum aufsteigenden Knoten der Bahn.
): Sie ist der Winkel
in der Ebene der Ekliptik zwischen der Richtung zum Frühlingspunkt
und der Richtung zum aufsteigenden Knoten der Bahn.
- Argument des Perihels (
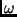 ): Das ist der Winkel in der
Bahnebene zwischen der Richtung zum aufsteigenden Knoten und der
Richtung zum Perihel (dem sonnennächsten Punkt der Bahn) und
definiert die Lage der großen Halbachse.
): Das ist der Winkel in der
Bahnebene zwischen der Richtung zum aufsteigenden Knoten und der
Richtung zum Perihel (dem sonnennächsten Punkt der Bahn) und
definiert die Lage der großen Halbachse.
- Bahnneigung (
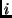 ): Sie ist der Winkel zwischen der Bahnebene und der Ebene
der Ekliptik, und bestimmt zusammen mit der Länge des aufsteigenden
Knotens die Lage der Bahnebene im Raum.
): Sie ist der Winkel zwischen der Bahnebene und der Ebene
der Ekliptik, und bestimmt zusammen mit der Länge des aufsteigenden
Knotens die Lage der Bahnebene im Raum.
- Numerische Exzentrizität der Bahn (
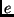 ) und
) und
- große Halbachse (
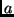 ): Diese beiden Größen definieren
die Form des Kegelschnitts. Bei Hyperbel- oder Parabelbahnen wird
statt dessen der Halbparameter
): Diese beiden Größen definieren
die Form des Kegelschnitts. Bei Hyperbel- oder Parabelbahnen wird
statt dessen der Halbparameter
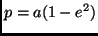 oder die Periheldistanz
oder die Periheldistanz 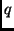 = 1/2
= 1/2 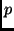 benutzt.
benutzt.
- Periheldurchgangszeit (
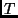 ): Die Zeit, zu der der Himmelskörper
durch das Perihel seiner Bahn läuft. Bei elliptischen Bahnen wird
die mittlere Anomalie
): Die Zeit, zu der der Himmelskörper
durch das Perihel seiner Bahn läuft. Bei elliptischen Bahnen wird
die mittlere Anomalie 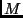 benutzt. Es gilt
benutzt. Es gilt
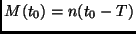 . Dazu
ist die Angabe der mittleren täglichen Bewegung
. Dazu
ist die Angabe der mittleren täglichen Bewegung 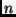 und einer
Epoche
und einer
Epoche 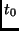 nötig.
nötig.




Next: Physikalische und geometrische Eigenschaften
Up: Grundlagen
Previous: Grundlagen
Contents
Juergen Weiprecht
2002-10-29