Next: Das allgemeine Keplerproblem
Up: Grundlagen
Previous: Grundlagen
Contents
Der Bewegungsablauf ist beim speziellen Zweikörperproblem mit
dem Kraftgesetz 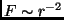 durch die
Anfangsbedingungen vollständig festgelegt. Die Anfangsbedingungen
sind im allgemeinsten Fall die Örter und Geschwindigkeiten beider
Körper zum Zeitpunkt
durch die
Anfangsbedingungen vollständig festgelegt. Die Anfangsbedingungen
sind im allgemeinsten Fall die Örter und Geschwindigkeiten beider
Körper zum Zeitpunkt 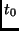 . Da wir uns nur für die Relativbewegung
des einen um den anderen Körper interessieren, können wir ohne
Einschränkung der Allgemeinheit den einen Körper in den Ursprung eines
neuen Koordinatensystems legen:
. Da wir uns nur für die Relativbewegung
des einen um den anderen Körper interessieren, können wir ohne
Einschränkung der Allgemeinheit den einen Körper in den Ursprung eines
neuen Koordinatensystems legen:
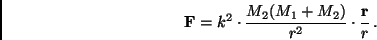 |
(2) |
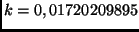 ist die GAUSSsche Gravitationskonstante (siehe auch
Aufgabe 13).
In diesem Koordinatensystem mit dem Ursprung in
ist die GAUSSsche Gravitationskonstante (siehe auch
Aufgabe 13).
In diesem Koordinatensystem mit dem Ursprung in 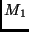 sind die
Anfangsbedingungen allein durch Ort und Geschwindigkeit des zweiten
Körpers gegeben, der sich auf einer KEPLERbahn um den Zentralkörper
bewegt. Der momentane Abstand
sind die
Anfangsbedingungen allein durch Ort und Geschwindigkeit des zweiten
Körpers gegeben, der sich auf einer KEPLERbahn um den Zentralkörper
bewegt. Der momentane Abstand 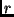 und der Betrag der dazugehörigen
Geschwindigkeit
und der Betrag der dazugehörigen
Geschwindigkeit 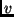 sind beim speziellen KEPLERproblem über den
Energieerhaltungssatz
sind beim speziellen KEPLERproblem über den
Energieerhaltungssatz
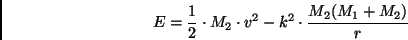 |
(3) |
miteinander verknüpft.
Mit Hilfe des Drehimpulserhaltungssatzes erhält man durch einfache
Umformungen (siehe auch [3]) die Geschwindigkeitsbeziehung:
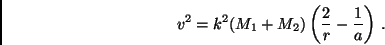 |
(4) |
Die Gleichung ist für alle möglichen Bahnformen gültig wenn man
vereinbart, daß die große Halbachse 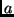 im Fall einer Hyperbelbahn
als negativ anzusehen ist. Da mit der großen Halbachse die Bahnform
eingeht, gibt es für einen bestimmten Kegelschnitt nur einen durch die
Gleichung definierten Parameterbereich von
im Fall einer Hyperbelbahn
als negativ anzusehen ist. Da mit der großen Halbachse die Bahnform
eingeht, gibt es für einen bestimmten Kegelschnitt nur einen durch die
Gleichung definierten Parameterbereich von 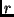 und
und 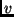 der die
entsprechende Bahnform liefert. Gleichung (4) kann man also benutzen, um
die Wertebereiche für die Anfangsbedingungen zu finden, die zu
den verschiedenen möglichen Bahnformen im speziellen KEPLERproblem
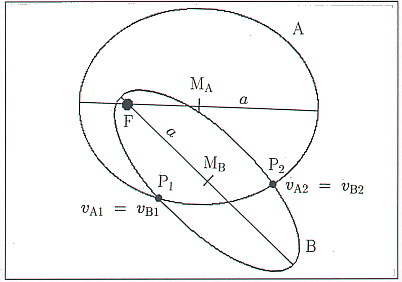
führen [4]. Man beachte, das die Geschwindigkeit des Körpers
mit der Masse
der die
entsprechende Bahnform liefert. Gleichung (4) kann man also benutzen, um
die Wertebereiche für die Anfangsbedingungen zu finden, die zu
den verschiedenen möglichen Bahnformen im speziellen KEPLERproblem
führen [4]. Man beachte, das die Geschwindigkeit des Körpers
mit der Masse 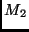 außer vom momentanen Abstand der beiden Massen
nur von der großen Halbachse abhängt (siehe Abb. 1).
Im Computerprogramm ist als Zeiteinheit
außer vom momentanen Abstand der beiden Massen
nur von der großen Halbachse abhängt (siehe Abb. 1).
Im Computerprogramm ist als Zeiteinheit
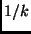 Tage gewählt worden. Die Masseneinheit ist die Sonnenmasse, die
Entfernungseinheit die astronomische Einheitsentfernung A.
Die Masse des Testkörpers wurde
vernachlässigt, wodurch sich die obige Gleichung noch zu
Tage gewählt worden. Die Masseneinheit ist die Sonnenmasse, die
Entfernungseinheit die astronomische Einheitsentfernung A.
Die Masse des Testkörpers wurde
vernachlässigt, wodurch sich die obige Gleichung noch zu
 |
(5) |
vereinfacht. Durch die Symmetrie des Problems ist es für eine
Simulation völlig ausreichend, den Körper bei einer Position 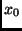 auf
der
auf
der 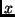 -Achse mit einer Geschwindigkeit
-Achse mit einer Geschwindigkeit 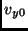 parallel zur
parallel zur 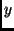 -Achse
zu starten. Diese Größen werden auch von dem Simulationsprogramm
als Eingabeparameter verlangt.
-Achse
zu starten. Diese Größen werden auch von dem Simulationsprogramm
als Eingabeparameter verlangt.




Next: Das allgemeine Keplerproblem
Up: Grundlagen
Previous: Grundlagen
Contents
Juergen Weiprecht
2002-10-29