Next: Auswertung der CCD-Aufnahmen
Up: Grundlagen
Previous: Das Zwei-Farben-Diagramm
Contents
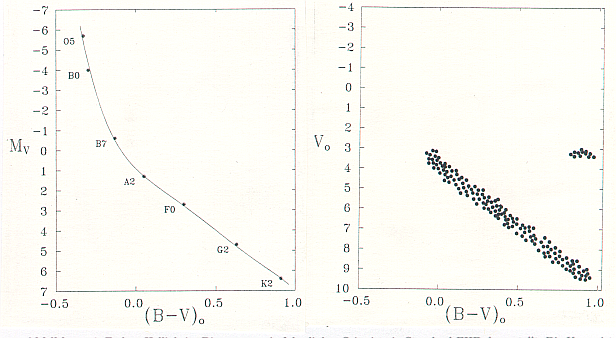
Das Farben-Helligkeits-Diagramm wird von den Eigenfarben und den
absoluten Helligkeiten der beobachteten Sterne aufgespannt. Bei der
Photometrie von Einzelsternen im 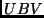 -System ist die absolute Helligkeit
nur aus zusätzlichen Informationen (Sternspektrum) zu erhalten.
Bei der Photometrie von Sternhaufen geht man mit den aus dem ZFD erhaltenen
Eigenfarben
-System ist die absolute Helligkeit
nur aus zusätzlichen Informationen (Sternspektrum) zu erhalten.
Bei der Photometrie von Sternhaufen geht man mit den aus dem ZFD erhaltenen
Eigenfarben 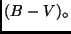 in ein FHD, dessen
in ein FHD, dessen 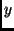 -Achse von der
Differenz
-Achse von der
Differenz 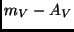 aufgespannt wird. Diese vom Einfluß der interstellaren
Extinktion befreite scheinbare Helligkeit wird mit
aufgespannt wird. Diese vom Einfluß der interstellaren
Extinktion befreite scheinbare Helligkeit wird mit 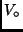 bezeichnet.
Entsprechend Gleichung (7) kann man also schreiben:
bezeichnet.
Entsprechend Gleichung (7) kann man also schreiben:
 |
(12) |
Ein Vergleich dieses Diagramms mit einem Standard-FHD, dessen y-Achse
durch 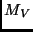 aufgespannt wird, liefert den Entfernungsmodul.
Man legt praktisch beide Diagramme in Abb. 4 übereinander und verschiebt
sie so lange in y-Richtung gegeneinander, bis beide Hauptreihen zur
Deckung kommen. Die Nullpunktsdifferenz der beiden y-Achsen ist gleich dem
Entfernungsmodul. Diese Art der Entfernungsbestimmung ist die Methode
der Sternhaufenparallaxen. Dieses Verfahren ist relativ genau,
weitreichend und von großer Bedeutung, da sich mit ihm die absoluten
Helligkeiten aller derjenigen Sterntypen bestimmen lassen, die durch
geometrische Entfernungsbestimmungsmethoden nicht erfaßt werden. Der
Sternhaufen, auf dem die Skala der absoluten Helligkeiten basiert und
der damit die Grundlage aller weiteren Entfernugsbestimmungen bildet,
sind die Hyaden. Die Entfernung dieses Haufens wurde mit der Methode
der Sternstromparallaxen zu
aufgespannt wird, liefert den Entfernungsmodul.
Man legt praktisch beide Diagramme in Abb. 4 übereinander und verschiebt
sie so lange in y-Richtung gegeneinander, bis beide Hauptreihen zur
Deckung kommen. Die Nullpunktsdifferenz der beiden y-Achsen ist gleich dem
Entfernungsmodul. Diese Art der Entfernungsbestimmung ist die Methode
der Sternhaufenparallaxen. Dieses Verfahren ist relativ genau,
weitreichend und von großer Bedeutung, da sich mit ihm die absoluten
Helligkeiten aller derjenigen Sterntypen bestimmen lassen, die durch
geometrische Entfernungsbestimmungsmethoden nicht erfaßt werden. Der
Sternhaufen, auf dem die Skala der absoluten Helligkeiten basiert und
der damit die Grundlage aller weiteren Entfernugsbestimmungen bildet,
sind die Hyaden. Die Entfernung dieses Haufens wurde mit der Methode
der Sternstromparallaxen zu
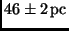 bestimmt. Durch
Beobachtung von Sternhaufen, die Sterne mit größeren absoluten Helligkeiten
enthalten, läßt sich dann die Hauptreihe weiter nach oben fortsetzen
(siehe auch Abb. 5).
Eine Schwierigkeit besteht jedoch darin, daß der Ort eines Sterns im
FHD (HRD) durch die Art seiner Energieerzeugung bestimmt wird, die
sich im Verlauf der Sternentwicklung (siehe z.B. in [8])
ändert. Der Weg, den ein Stern im FHD dabei zurücklegt, ist durch seine
Masse und seine chemische Zusammensetzung vorgegeben. Die
meiste Zeit verbringen alle Sterne auf der Hauptreihe. Danach bewegen
sie sich zunächst im FHD nach rechts. Das geschieht um so schneller,
je größer die Masse eines Sterns und um so größer damit auch seine
absolute Helligkeit ist (Masse-Leuchtkraft-Gesetz). Die Hauptreihe
erhält durch diese Positionsänderung einen typischen Knick, dessen Lage
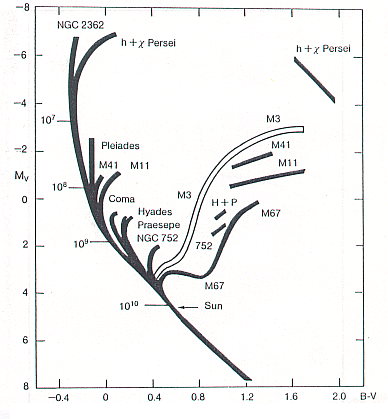
im FHD durch das Alter des Sternhaufens bestimmt ist. In Abb. 5 ist ein
schematisches FHD für Sternhaufen unterschiedlichen Alters und damit
unterschiedlicher Lage des Abknickpunktes (engl.: Turnoff Point)
dargestellt.
Aus Abb. 5 läßt sich entnehmen, daß für Farbenindizes größer als
bestimmt. Durch
Beobachtung von Sternhaufen, die Sterne mit größeren absoluten Helligkeiten
enthalten, läßt sich dann die Hauptreihe weiter nach oben fortsetzen
(siehe auch Abb. 5).
Eine Schwierigkeit besteht jedoch darin, daß der Ort eines Sterns im
FHD (HRD) durch die Art seiner Energieerzeugung bestimmt wird, die
sich im Verlauf der Sternentwicklung (siehe z.B. in [8])
ändert. Der Weg, den ein Stern im FHD dabei zurücklegt, ist durch seine
Masse und seine chemische Zusammensetzung vorgegeben. Die
meiste Zeit verbringen alle Sterne auf der Hauptreihe. Danach bewegen
sie sich zunächst im FHD nach rechts. Das geschieht um so schneller,
je größer die Masse eines Sterns und um so größer damit auch seine
absolute Helligkeit ist (Masse-Leuchtkraft-Gesetz). Die Hauptreihe
erhält durch diese Positionsänderung einen typischen Knick, dessen Lage
im FHD durch das Alter des Sternhaufens bestimmt ist. In Abb. 5 ist ein
schematisches FHD für Sternhaufen unterschiedlichen Alters und damit
unterschiedlicher Lage des Abknickpunktes (engl.: Turnoff Point)
dargestellt.
Aus Abb. 5 läßt sich entnehmen, daß für Farbenindizes größer als
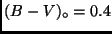 - das entspricht dem Spektraltyp F3 - sich die Sterne
noch nicht von der Hauptreihe entfernt haben. Bei einer photometrischen
Entfernungsbestimmung ist unbedingt darauf zu achten, daß die Hauptreihe
unterhalb des Abknickpunktes angepaßt wird.
Ein weiteres Problem stellt die unterschiedliche chemische Zusammensetzung
der Sterne dar. Es gibt Sterne, bei denen die schweren Elemente (gemeint
sind Elemente schwerer als Helium) bis zu dreimal häufiger sind als in
der Sonne, aber auch solche, bei denen die relative Häufigkeit weniger
als
- das entspricht dem Spektraltyp F3 - sich die Sterne
noch nicht von der Hauptreihe entfernt haben. Bei einer photometrischen
Entfernungsbestimmung ist unbedingt darauf zu achten, daß die Hauptreihe
unterhalb des Abknickpunktes angepaßt wird.
Ein weiteres Problem stellt die unterschiedliche chemische Zusammensetzung
der Sterne dar. Es gibt Sterne, bei denen die schweren Elemente (gemeint
sind Elemente schwerer als Helium) bis zu dreimal häufiger sind als in
der Sonne, aber auch solche, bei denen die relative Häufigkeit weniger
als 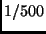 des Wertes der Sonne beträgt. Diese großen Unterschiede
lassen sich im Rahmen einer Kosmogonie des Milchstraßensystems erklären
(siehe hierzu z.B. [9]). In der Astronomie wird die relative Häufigkeit
der Elemente schwerer als Helium oft als Metallgehalt bezeichnet.
Eine unterschiedliche Metallhäufigkeit macht sich in einer etwas geänderten
Lage der Hauptreihe - sie liegt je nach chemischer Zusammensetzung bei
etwas größeren oder kleineren absoluten Helligkeiten als eine Hauptreihe
mit solaren Häufigkeiten - bemerkbar. Da das Abknicken der Hauptreihe relativ
flach verläuft, kann sich ein abweichender Metallgehalt oder ein Meßfehler
in den Farben oder den Helligkeiten sehr stark auf die Altersbestimmung,
jedoch nicht so stark auf die Entfernungsbestimmung auswirken. Man kann
abschätzen, daß ein systematischer Fehler in
des Wertes der Sonne beträgt. Diese großen Unterschiede
lassen sich im Rahmen einer Kosmogonie des Milchstraßensystems erklären
(siehe hierzu z.B. [9]). In der Astronomie wird die relative Häufigkeit
der Elemente schwerer als Helium oft als Metallgehalt bezeichnet.
Eine unterschiedliche Metallhäufigkeit macht sich in einer etwas geänderten
Lage der Hauptreihe - sie liegt je nach chemischer Zusammensetzung bei
etwas größeren oder kleineren absoluten Helligkeiten als eine Hauptreihe
mit solaren Häufigkeiten - bemerkbar. Da das Abknicken der Hauptreihe relativ
flach verläuft, kann sich ein abweichender Metallgehalt oder ein Meßfehler
in den Farben oder den Helligkeiten sehr stark auf die Altersbestimmung,
jedoch nicht so stark auf die Entfernungsbestimmung auswirken. Man kann
abschätzen, daß ein systematischer Fehler in 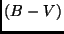 um 0.01 mag das Alter
um 7% verfälschen kann. Den gleichen Effekt hat ein um 10% von der
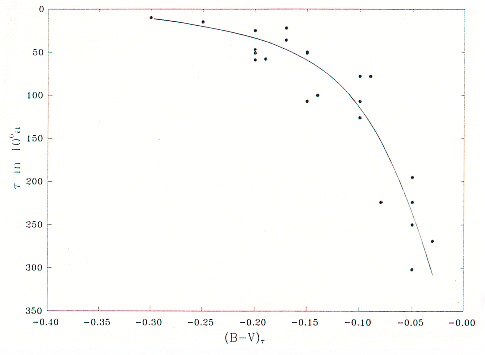
solaren Häufigkeit abweichender Metallgehalt. In Abb. 6 ist das Alter
von Sternhaufen in Abhängigkeit vom Farbenindex des Abknickpunktes für
den Fall solarer Metallhäufigkeit dargestellt.
Eine weitere etwas genauere Methode ist die Isochronenanpassung.
Hierbei werden die Beobachtungen mit Sternentwicklungsrechnungen verglichen.
Eine Isochrone wird aus Sternentwicklungsrechnungen für Sterne
unterschiedlicher Masse zusammengesetzt. Sie verbindet alle Punkte
gleichen Alters im FHD.
um 0.01 mag das Alter
um 7% verfälschen kann. Den gleichen Effekt hat ein um 10% von der
solaren Häufigkeit abweichender Metallgehalt. In Abb. 6 ist das Alter
von Sternhaufen in Abhängigkeit vom Farbenindex des Abknickpunktes für
den Fall solarer Metallhäufigkeit dargestellt.
Eine weitere etwas genauere Methode ist die Isochronenanpassung.
Hierbei werden die Beobachtungen mit Sternentwicklungsrechnungen verglichen.
Eine Isochrone wird aus Sternentwicklungsrechnungen für Sterne
unterschiedlicher Masse zusammengesetzt. Sie verbindet alle Punkte
gleichen Alters im FHD.




Next: Auswertung der CCD-Aufnahmen
Up: Grundlagen
Previous: Das Zwei-Farben-Diagramm
Contents
Juergen Weiprecht
2002-10-29