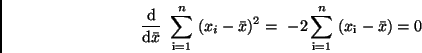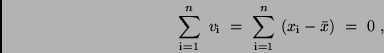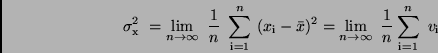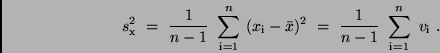Next: Indirekt bestimmte Beobachtungsgrößen, Fehlerfortpflanzung
Up: Rechnerische Erfassung zufälliger Fehler
Previous: Rechnerische Erfassung zufälliger Fehler
Contents
Der wahre Wert 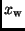 einer Beobachtungsgröße ist im
allgemeinen nicht angebbar. Man kennt nur die nach einer bestimmten
Meßvorschrift ermittelten
einer Beobachtungsgröße ist im
allgemeinen nicht angebbar. Man kennt nur die nach einer bestimmten
Meßvorschrift ermittelten 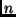 Beobachtungswerte
Beobachtungswerte
Als Näherungswert für 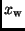 benutzt man das arithmetische
Mittel
benutzt man das arithmetische
Mittel
 |
(9) |
Es erfüllt die GAUSSsche Bedingung der kleinsten Summe der Fehlerquadrate,
d.h. die Summe der Quadrate der scheinbaren Fehler
 |
(10) |
also
 |
(11) |
ist ein Minimum. Aus der Extremalbedingung
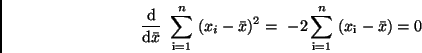 |
(12) |
folgt nämlich
und damit (9). Darüber hinaus erfüllt das arithmetische Mittel die Bedingung,
daß die Summe der scheinbaren Fehler verschwindet.
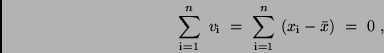 |
(13) |
was man aus (12) erkennt.
Der Vergleich von (9) mit (3) zeigt, daß bei der Bildung des arithmetischen
Mittels jedem Beobachtungswert 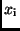 die gleiche Wahrscheinlichkeit
die gleiche Wahrscheinlichkeit
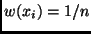 zugeordnet wird. Für den Grenzfall unendlich vieler
Beobachtungen
zugeordnet wird. Für den Grenzfall unendlich vieler
Beobachtungen
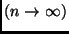 würde sich die Standardabweichung
würde sich die Standardabweichung
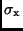 nach (5) zu
nach (5) zu
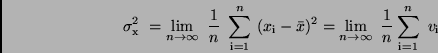 |
(14) |
ergeben. Grundsätzlich existieren aber immer nur endlich viele Beobachtungen.
Um den Meßwert dennoch eine Standardabweichung 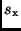 zuordnen zu können,
definiert man
zuordnen zu können,
definiert man
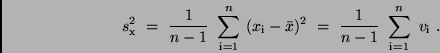 |
(15) |
Diese Festlegung sichert, daß im Grenzfall
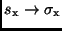 geht, und daß
einem einzigen Beobachtungswert
geht, und daß
einem einzigen Beobachtungswert 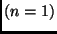 keine Standardabweichung zukommt.
Dies wäre auch nicht sinnvoll, da ja bei einer einzigen Beobachtung keine
Vergleichsmöglichkeiten existieren.
keine Standardabweichung zukommt.
Dies wäre auch nicht sinnvoll, da ja bei einer einzigen Beobachtung keine
Vergleichsmöglichkeiten existieren. 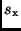 bezeichnet man als die
Standardabweichung einer Einzelmessung oder als den mittleren
quadratischen Fehler einer Einzelmessung.
Bei einer genügend großen Anzahl von Beobachtungen und beim Vorliegen einer
Normalverteilung läßt sich die statistische Sicherheit
bezeichnet man als die
Standardabweichung einer Einzelmessung oder als den mittleren
quadratischen Fehler einer Einzelmessung.
Bei einer genügend großen Anzahl von Beobachtungen und beim Vorliegen einer
Normalverteilung läßt sich die statistische Sicherheit
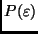 angeben,
mit der die Messungen in dem Bereich
angeben,
mit der die Messungen in dem Bereich
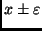 um den Mittelwert
liegen. Sie entspricht den in der Tabelle 1 angegebenen Wahrscheinlichkeiten
um den Mittelwert
liegen. Sie entspricht den in der Tabelle 1 angegebenen Wahrscheinlichkeiten
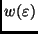 , wenn man nur
, wenn man nur
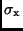 durch
durch 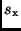 ersetzt. Für
ersetzt. Für
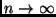 gilt
gilt
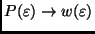 .
.




Next: Indirekt bestimmte Beobachtungsgrößen, Fehlerfortpflanzung
Up: Rechnerische Erfassung zufälliger Fehler
Previous: Rechnerische Erfassung zufälliger Fehler
Contents
Juergen Weiprecht
2002-10-29