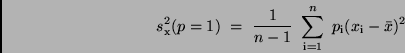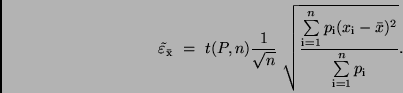Next: Lineare Ausgleichung von Beobachtungen
Up: Rechnerische Erfassung zufälliger Fehler
Previous: Mittlerer Fehler und statistische
Contents
Haben die Beobachtungswerte 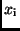 nicht alle die gleiche Genauigkeit,
so ordnet man ihnen entsprechend der jeweiligen Genauigkeit unterschiedliche
Gewichte
nicht alle die gleiche Genauigkeit,
so ordnet man ihnen entsprechend der jeweiligen Genauigkeit unterschiedliche
Gewichte 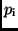 zu. Je höher die Genauigkeit ist, um so größer ist das
Gewicht der Beobachtung. Die Wahrscheinlichkeit, mit der der Beobachtungswert
zu. Je höher die Genauigkeit ist, um so größer ist das
Gewicht der Beobachtung. Die Wahrscheinlichkeit, mit der der Beobachtungswert
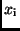 auftritt, ist dann nicht mehr
auftritt, ist dann nicht mehr
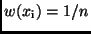 , sondern
, sondern
und das arithmetische Mittel ergibt sich demzufolge zu
Die der Gleichung (12) entsprechende Extremalbedingung liefert
Die Standardabweichung der Einzelbeobachtungen bezieht man im allgemeinen
auf eine Beobachtung des Gewichts 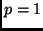 , so daß man
, so daß man
erhält. Schließlich benötigt man noch zur Berechnung der Vertrauensintervalle
bei vorgegebener statistischer Sicherheit 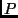 die Größe von
die Größe von
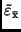 . Sie berechnet sich zu
. Sie berechnet sich zu
Juergen Weiprecht
2002-10-29