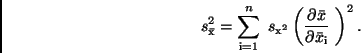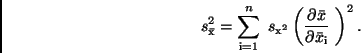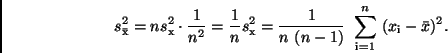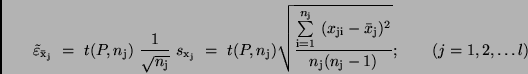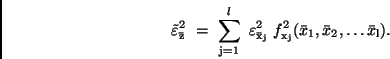Next: Beobachtungen unterschiedlicher Genauigkeit
Up: Rechnerische Erfassung zufälliger Fehler
Previous: Indirekt bestimmte Beobachtungsgrößen, Fehlerfortpflanzung
Contents
Mittels des Fehlerfortpflanzungsgesetzes und der Standardabweichung 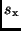 einer Einzelbeobachtung läßt sich der mittlere Fehler
einer Einzelbeobachtung läßt sich der mittlere Fehler
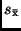 des
arithmetischen Mittels (Standardabweichung des arithmetischen Mittels)
bestimmen. Er ergibt sich zu
des
arithmetischen Mittels (Standardabweichung des arithmetischen Mittels)
bestimmen. Er ergibt sich zu
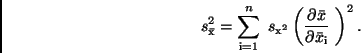 |
(27) |
Für die partiellen Ableitungen erhält man nach (9)
Unter Verwendung von (15) folgt daraus, da 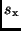 für alle
Beobachtungen gleich ist,
für alle
Beobachtungen gleich ist,
Während sich durch die Erhöhung der Anzahl 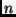 der Beobachtungen die
Standardabweichung der Einzelbeobachtungen nicht verkleinern läßt
-
in (15) kommt für jeden neuen Beobachtungswert ein Summand hinzu - ist dies
bezüglich des arithmetischen Mittels möglich. Die Standardabweichung
der Beobachtungen die
Standardabweichung der Einzelbeobachtungen nicht verkleinern läßt
-
in (15) kommt für jeden neuen Beobachtungswert ein Summand hinzu - ist dies
bezüglich des arithmetischen Mittels möglich. Die Standardabweichung
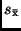 sinkt aber nur proportional zu
sinkt aber nur proportional zu 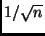 .
Das arithmetische Mittel wird meist als endgültiges Beobachtungsergebnis
angesehen. Es ist aber im allgemeinen nicht mit dem wahren Wert der
Beobachtungsgröße identisch. Mit einer bestimmten statistischen Sicherheit
.
Das arithmetische Mittel wird meist als endgültiges Beobachtungsergebnis
angesehen. Es ist aber im allgemeinen nicht mit dem wahren Wert der
Beobachtungsgröße identisch. Mit einer bestimmten statistischen Sicherheit
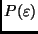 befindet sich (bei Abwesenheit systematischer Fehler) der
wahre Wert in einem Intervall
befindet sich (bei Abwesenheit systematischer Fehler) der
wahre Wert in einem Intervall
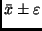 um den Mittelwert.
Die Intervallgröße ist von der Höhe von
um den Mittelwert.
Die Intervallgröße ist von der Höhe von  anhängig: Je größere
Sicherheitsforderungen man stellt, um so größer ist zwangsläufig das
Intervall, in dem der wahre Wert liegen kann. Zur Bestimmung von
anhängig: Je größere
Sicherheitsforderungen man stellt, um so größer ist zwangsläufig das
Intervall, in dem der wahre Wert liegen kann. Zur Bestimmung von
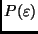 kann man wieder die Tabelle 1 benutzen, nur muß man jetzt
kann man wieder die Tabelle 1 benutzen, nur muß man jetzt 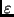 in
Vielfachen von
in
Vielfachen von
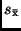 , des mittleren Fehlers des arithmetischen
Mittels, angeben,
, des mittleren Fehlers des arithmetischen
Mittels, angeben,
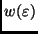 geht dann in
geht dann in
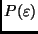 über. Das
Intervall
über. Das
Intervall
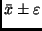 wird als Vertrauensintervall des
arithmetischen Mittels bei vorgegebener statistischer Sicherheit
wird als Vertrauensintervall des
arithmetischen Mittels bei vorgegebener statistischer Sicherheit
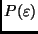 bezeichnet.
Bei allen bisherigen Überlegungen wurde eine sehr große Anzahl
bezeichnet.
Bei allen bisherigen Überlegungen wurde eine sehr große Anzahl 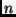 von
Beobachtungen vorausgesetzt. Vielfach ist das aber in der Realität nicht
erreichbar. Je kleiner
von
Beobachtungen vorausgesetzt. Vielfach ist das aber in der Realität nicht
erreichbar. Je kleiner 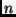 ist, um so stärker weicht die tatsächliche
Verteilung der Beobachtungsfehler von der GAUSS-Verteilung (und
entsprechend
ist, um so stärker weicht die tatsächliche
Verteilung der Beobachtungsfehler von der GAUSS-Verteilung (und
entsprechend
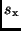 von
von
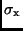 ) ab. Im Falle kleiner
) ab. Im Falle kleiner 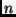 beschreibt man
die
Fehlerverteilung durch die sogenannte t-Verteilung (oder STUDENT-Verteilung),
auf die hier aber nicht im einzelnen eingegangen werden kann.
Es soll nur angegeben werden, wie sich für eine bestimmte, vorgegebene
statistische Sicherheit
beschreibt man
die
Fehlerverteilung durch die sogenannte t-Verteilung (oder STUDENT-Verteilung),
auf die hier aber nicht im einzelnen eingegangen werden kann.
Es soll nur angegeben werden, wie sich für eine bestimmte, vorgegebene
statistische Sicherheit 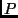 die Größe des Vertrauensintervalls
die Größe des Vertrauensintervalls
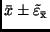 bei kleinem
bei kleinem 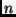 ergibt. Es gilt
ergibt. Es gilt
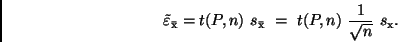 |
(28) |
Dabei ist 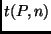 ein Korrekturfaktor, der von der Höhe der vorgegebenen
statistischen Sicherheit
ein Korrekturfaktor, der von der Höhe der vorgegebenen
statistischen Sicherheit 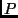 und der Anzahl
und der Anzahl 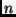 der zur Verfügung stehenden
Beobachtungen abhängt. In der Tabelle 2 ist
der zur Verfügung stehenden
Beobachtungen abhängt. In der Tabelle 2 ist 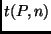 für einige
für einige 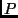 - und
- und 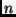 -Werte
angegeben. Der Vergleich mit Tabelle 1 zeigt, daß für sehr große
-Werte
angegeben. Der Vergleich mit Tabelle 1 zeigt, daß für sehr große
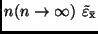 in
in
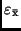 übergeht.
Ist die gesuchte Größe
übergeht.
Ist die gesuchte Größe 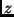 nur indirekt zu ermitteln, so errechnet man
zunächst für die einzelnen Beobachtungsgrößen
nur indirekt zu ermitteln, so errechnet man
zunächst für die einzelnen Beobachtungsgrößen
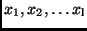 die
Größe des Vertrauensintervalls
die
Größe des Vertrauensintervalls
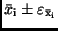 um
die jeweiligen arithmetischen Mittel bei vorgegebener statistischer
Sicherheit
um
die jeweiligen arithmetischen Mittel bei vorgegebener statistischer
Sicherheit 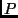 :
:
In Analogie zu (26) ergibt sich aus diesen Werten die Größe des
Vertrauensintervalls
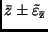 mit
mit
Bei der Berechnung des arithmetischen Mittels 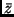 benutzt man formal
benutzt man formal
Tabelle 2: Die STUDENT-Verteilung für eine kleine
Anzahl 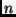 von Beobachtungen. Wahrscheinlichkeiten dafür, daß ein Zufallsereignis
innerhalb vorgegebener Intervallgrenzen liegt.
von Beobachtungen. Wahrscheinlichkeiten dafür, daß ein Zufallsereignis
innerhalb vorgegebener Intervallgrenzen liegt.
| |
P = 68,3% |
P = 95,0% |
P = 99,0% |
P = 99,7% |
| n |
t |
t/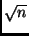 |
t |
T/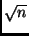 |
t |
t/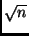 |
t |
t/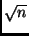 |
| |
|
|
|
|
|
|
|
|
| 2 |
1,80 |
1,270 |
12,70 |
9,00 |
64,0 |
45,30 |
235,0 |
166,20 |
| 3 |
1,32 |
0,762 |
4,30 |
2,50 |
9,9 |
5,70 |
19,2 |
11,10 |
| 4 |
1,20 |
0,600 |
3,20 |
1,60 |
5,8 |
2,90 |
9,2 |
4,60 |
| 5 |
1,15 |
0.514 |
2,80 |
1,20 |
4,6 |
2,10 |
6,6 |
3,00 |
| 6 |
1,11 |
0,453 |
2,60 |
1,10 |
4,0 |
1,70 |
5,5 |
2,30 |
| 8 |
1,08 |
0,382 |
2,40 |
0,84 |
3,5 |
1,20 |
4,5 |
1,60 |
| 10 |
1,06 |
0,335 |
2,30 |
0,72 |
3,2 |
1,00 |
4,1 |
1,30 |
| 20 |
1,03 |
0,230 |
2,10 |
0,47 |
2,9 |
0,64 |
3,4 |
0,77 |
| 30 |
1,02 |
0,186 |
2,00 |
0,37 |
2,8 |
0,50 |
3,3 |
0,60 |
| 50 |
1,01 |
0,143 |
2,00 |
0,28 |
2,7 |
0,38 |
3,2 |
0,45 |
| 100 |
1,00 |
0,100 |
2,00 |
0,20 |
2,6 |
0,26 |
3,1 |
0,31 |
| 200 |
1,00 |
0,071 |
1,99 |
0,14 |
2,6 |
0,18 |
3,0 |
0,21 |
n 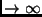 |
t 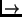 1 1 |
|
t 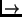 1,96 1,96 |
|
t 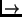 2,58 2,58 |
|
t 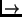 3 3 |
|




Next: Beobachtungen unterschiedlicher Genauigkeit
Up: Rechnerische Erfassung zufälliger Fehler
Previous: Indirekt bestimmte Beobachtungsgrößen, Fehlerfortpflanzung
Contents
Juergen Weiprecht
2002-10-29