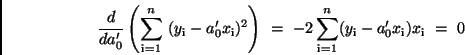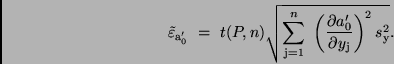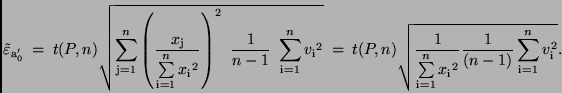Next: Allgemeine lineare Abhängigkeit von
Up: Lineare Ausgleichung von Beobachtungen
Previous: Lineare Ausgleichung von Beobachtungen
Contents
Aus der astronomischen Problemstellung sei bekannt (oder ist zu erwarten), daß
zwischen 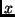 und
und 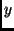 eine reine Proportionalität besteht. Es muß dann auch die
ausgleichende Gerade diese Bedingung erfüllen. Für sie muß also gelten
eine reine Proportionalität besteht. Es muß dann auch die
ausgleichende Gerade diese Bedingung erfüllen. Für sie muß also gelten
Damit ergeben sich die scheinbaren Fehler zu
und aus der GAUSSschen Bedingung folgt, daß 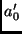 die Gleichung
die Gleichung
erfüllen muß. Aus ihr erhält man für den Proportionalitätsfaktor 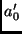
 |
(31) |
Der so berechnete Wert von 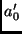 wird mit dem wahren
Proportionalitätsfaktor, der dem exakten physikalischen Zusammenhang von
wird mit dem wahren
Proportionalitätsfaktor, der dem exakten physikalischen Zusammenhang von 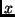 und
und 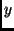 entsprecht, nicht identisch sein. Man kann aber wieder ein
Vertrauensintervall
entsprecht, nicht identisch sein. Man kann aber wieder ein
Vertrauensintervall
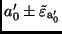 angeben, in dem
der wahre Wert mit vorgegebener statistischer Sicherheit
angeben, in dem
der wahre Wert mit vorgegebener statistischer Sicherheit 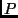 liegt. Zur
Berechnung von
liegt. Zur
Berechnung von
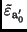 geht man in der gleichen Weise
vor wie bei der Berechnung der Standardabweichung und des Vertrauensintervalls
für das arithmetische Mittel. In Analogie zu (27) und (28) ergibt sich
geht man in der gleichen Weise
vor wie bei der Berechnung der Standardabweichung und des Vertrauensintervalls
für das arithmetische Mittel. In Analogie zu (27) und (28) ergibt sich
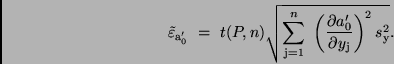 |
(32) |
Für die partiellen Ableitungen erhält man auf Grund von (31)
und für die Standardabweichung 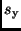 der
der 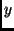 -Werte entsprechend (15)
-Werte entsprechend (15)
 |
(33) |
Setzt man dies in (32) ein, so ergibt sich schließlich
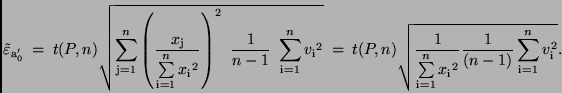 |
(34) |




Next: Allgemeine lineare Abhängigkeit von
Up: Lineare Ausgleichung von Beobachtungen
Previous: Lineare Ausgleichung von Beobachtungen
Contents
Juergen Weiprecht
2002-10-29