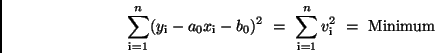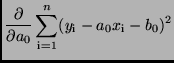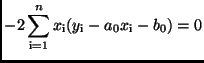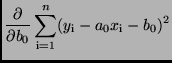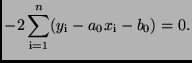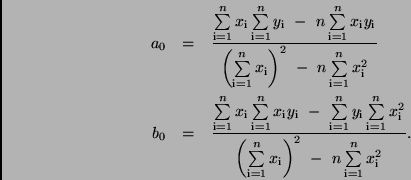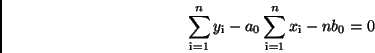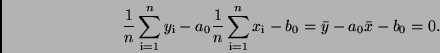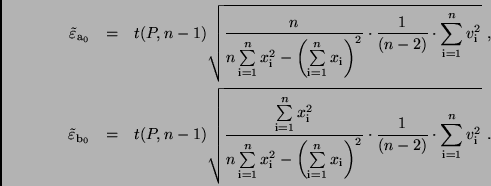Next: Systematische Fehler, Größtfehler
Up: Lineare Ausgleichung von Beobachtungen
Previous: Proportionalität von und
Contents
Bei einer allgemeinen linearen Abhängigkeit zwischen den Beobachtungsgrößen
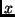 und
und 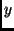 in der Form von (29) sind durch eine Ausgleichung die beiden
Konstanten
in der Form von (29) sind durch eine Ausgleichung die beiden
Konstanten 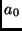 und
und 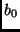 zu ermitteln. Die GAUSSsche Bedingung
zu ermitteln. Die GAUSSsche Bedingung
führt auf die beiden Gleichungen
Löst man sie nach 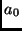 und
und 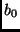 auf, so erhält man
auf, so erhält man
Schreibt man Gleichung (35) in
um, so ergibt sich daraus
Der Mittelpunkt
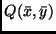 der
der 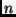 Wertepaare
Wertepaare
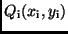 liegt also auf der ausgleichenden Geraden. Hat man daher
liegt also auf der ausgleichenden Geraden. Hat man daher 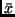 und
und
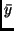 sowie
sowie 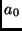 und
und 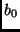 berechnet, so müssen diese Werte die
Gleichung (30) erfüllen.
Zur Berechnung der Größe der Vertrauensintervalle
berechnet, so müssen diese Werte die
Gleichung (30) erfüllen.
Zur Berechnung der Größe der Vertrauensintervalle
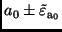 und
und
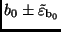 bei vorgegebener
statistischer Sicherheit
bei vorgegebener
statistischer Sicherheit 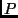 benötigt man die Standardabweichung
benötigt man die Standardabweichung 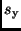 der
der
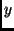 -Werte. Sie ist definiert durch
-Werte. Sie ist definiert durch
Dieser Ansatz bewirkt, daß 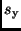 bereits unendlich groß wird, wenn nur zwei
Beobachtungen, also zwei Wertepaare
bereits unendlich groß wird, wenn nur zwei
Beobachtungen, also zwei Wertepaare
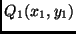 und
und
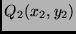 vorliegen. Bei der Ausgleichung geht man ja davon aus,
daß die Beobachtungswerte um eine ausgleichende Gerade streuen. Durch zwei
Punkte in der
vorliegen. Bei der Ausgleichung geht man ja davon aus,
daß die Beobachtungswerte um eine ausgleichende Gerade streuen. Durch zwei
Punkte in der 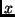 -
-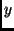 -Ebene wäre aber eine Gerade eindeutig festgelegt. Sie
geht durch beide Punkte, so daß der Begriff der Standardabweichung sinnlos
ist.
Entsprechende Überlegungen haben bei der Definition (15) im übrigen zu dem
Nenner
-Ebene wäre aber eine Gerade eindeutig festgelegt. Sie
geht durch beide Punkte, so daß der Begriff der Standardabweichung sinnlos
ist.
Entsprechende Überlegungen haben bei der Definition (15) im übrigen zu dem
Nenner 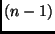 geführt. Wenn in der Definition (33) von
geführt. Wenn in der Definition (33) von 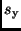 auch im Nenner
auch im Nenner
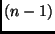 und nicht
und nicht 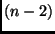 steht, so ist das dadurch bedingt, daß im Falle
einer reinen Proportionalität zwischen
steht, so ist das dadurch bedingt, daß im Falle
einer reinen Proportionalität zwischen 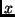 und
und 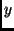 die ausgleichende
Beobachtung
die ausgleichende
Beobachtung 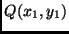 (zusammen mit dem Nullpunkt) schon eine Gerade
festlegt. Jede weitere Beobachtung (also auch schon die zweite) gibt die
Möglichkeit zur Berechnung der Standardabweichung der ausgleichenden Geraden.
Unter Anwendung des Fehlerfortpflanzungsgesetzes erhält man auf Grund
eines analogen Verfahrens, das zu (34) geführt hat, für
(zusammen mit dem Nullpunkt) schon eine Gerade
festlegt. Jede weitere Beobachtung (also auch schon die zweite) gibt die
Möglichkeit zur Berechnung der Standardabweichung der ausgleichenden Geraden.
Unter Anwendung des Fehlerfortpflanzungsgesetzes erhält man auf Grund
eines analogen Verfahrens, das zu (34) geführt hat, für
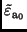 und
und
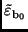
In dem Korrekturfaktor 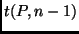 ist ebenfalls berücksichtigt, daß zur
Berechnung der Standardabweichungen der Koeffizienten
ist ebenfalls berücksichtigt, daß zur
Berechnung der Standardabweichungen der Koeffizienten 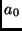 und
und 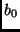 jeweils eine Beobachtung weniger zur Verfügung steht. Setzt man wieder
jeweils eine Beobachtung weniger zur Verfügung steht. Setzt man wieder
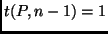 , gehen formal
, gehen formal
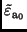 und
und
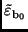 in
in 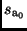 und
und  , die mittleren Fehler von
, die mittleren Fehler von
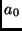 und
und
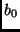 , über.
, über.




Next: Systematische Fehler, Größtfehler
Up: Lineare Ausgleichung von Beobachtungen
Previous: Proportionalität von und
Contents
Juergen Weiprecht
2002-10-29