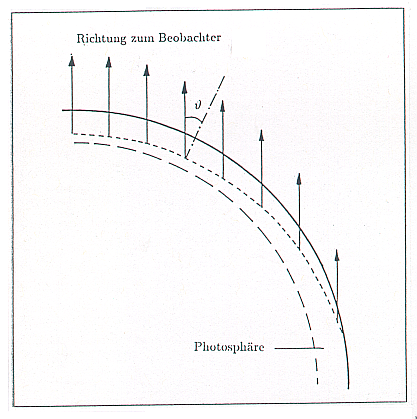



| (1) |
| (2) |
| (3) |
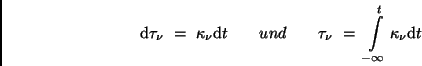 |
(4) |
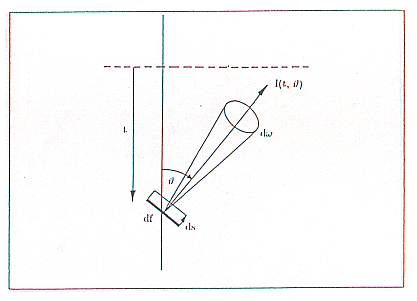

| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
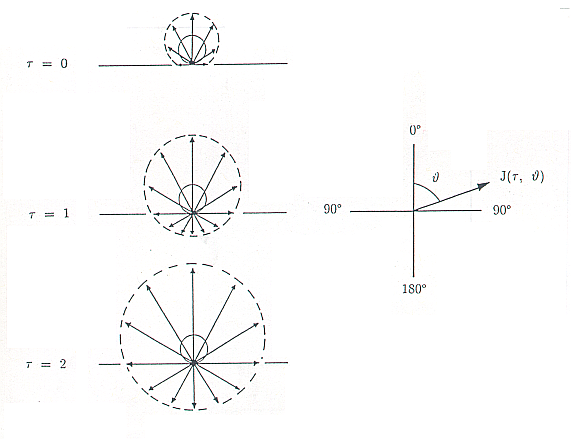


| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
|
|
|
|
| 0,000 | 1,000 | 1,00 |
| 0,200 | 0,980 | 0,99 |
| 0,400 | 0,916 | 0,95 |
| 0,550 | 0,835 | 0,90 |
| 0,650 | 0,760 | 0,86 |
| 0,750 | 0,661 | 0,80 |
| 0,875 | 0,484 | 0,69 |
| 0,950 | 0,312 | 0,59 |
| 0,975 | 0,222 | 0,53 |
| 1,000 | 0,000 | 0,40 |