



Next: Reduktion der Beobachtungen
Up: Grundlagen
Previous: Physikalische und geometrische Eigenschaften
Contents
GAUSS ging von der rein geometrischen Beziehung,
 |
(11) |
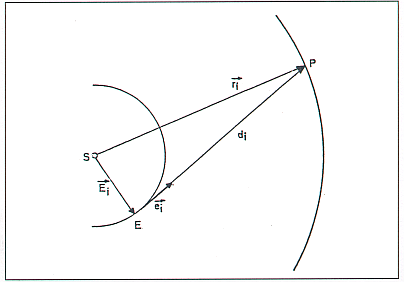
aus. Die Vektoren sind in Abbildung 2 dargestellt und erklärt.
Wie schon weiter oben gezeigt wurde, ist die Angabe von Orts- und
Geschwindigkeitsvektor
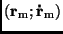 eines
Himmelskörpers zu einem
Zeitpunkt
eines
Himmelskörpers zu einem
Zeitpunkt 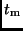 gleichwertig mit der Angabe der klassischen Bahnelemente beim
ungestörten Zweikörperproblem. Da
gleichwertig mit der Angabe der klassischen Bahnelemente beim
ungestörten Zweikörperproblem. Da
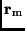 und
und
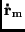 ,
wenn man die Möglichkeit des freien Falls in die Sonne ausschließt,
linear unabhängig sind und in der Bahnebene liegen, läßt sich auch
jeder andere Vektor in der Bahnebene
,
wenn man die Möglichkeit des freien Falls in die Sonne ausschließt,
linear unabhängig sind und in der Bahnebene liegen, läßt sich auch
jeder andere Vektor in der Bahnebene
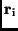 und
und
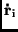 als Linearkombination von
als Linearkombination von
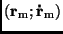 aufschreiben.
Liegen n Beobachtungen des topozentrischen
Einheitsvektors
aufschreiben.
Liegen n Beobachtungen des topozentrischen
Einheitsvektors
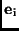 zu den Zeiten
zu den Zeiten
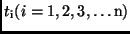 vor,
und bezeichnen wir die Koeffizienten der Ortsvektoren mit
vor,
und bezeichnen wir die Koeffizienten der Ortsvektoren mit
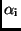 und die der Geschwindigkeitsvektoren mit
und die der Geschwindigkeitsvektoren mit 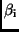 , so gilt:
, so gilt:
 |
(12) |
Die Werte für
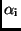 und
und
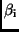 kann man sich durch eine
TAYLORreihenentwicklung nach
kann man sich durch eine
TAYLORreihenentwicklung nach
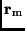 verschaffen. Man erhält:
verschaffen. Man erhält:
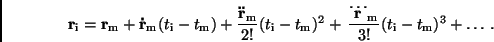 |
(13) |
Ersetzt man
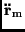 und
und
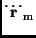 mit Hilfe der Bewegungsgleichung (1) und deren Ableitung und bricht die
Reihenentwicklung nach dem 3. Glied ab, erhält man:
mit Hilfe der Bewegungsgleichung (1) und deren Ableitung und bricht die
Reihenentwicklung nach dem 3. Glied ab, erhält man:
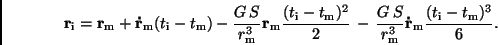 |
(14) |
Ein Koeffizientenvergleich zwischen Gl.(12) und Gl.(14) ergibt:
Setzt man Gl.(12) in Gl.(11) ein, so ergibt sich:
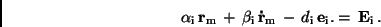 |
(17) |
Im Fall von 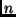 Beobachtungen handelt es sich dabei um ein lineares
Gleichungssystem mit
Beobachtungen handelt es sich dabei um ein lineares
Gleichungssystem mit 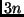 Gleichungen und
Gleichungen und 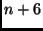 Unbekannten.
Im Fall von drei Beobachtungen ist dieses System eindeutig und
sofort lösbar. Im Fall
Unbekannten.
Im Fall von drei Beobachtungen ist dieses System eindeutig und
sofort lösbar. Im Fall 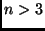 Beobachtungen haben wir mehr Gleichungen als
Unbekannte. In diesem Fall ist die Lösung durch Ausgleichsrechnung zu
erhalten. Dazu ist das Gleichungssystem in das entsprechende System von
Normalgleichungen zu überführen. Die dazu erforderlichen Rechenschritte
lassen sich am einfachsten erläutern, aber auch für das Abarbeiten im
Computer am übersichtlichsten darstellen, wenn man zur Matritzenschreibweise
übergeht.
Gl. (17) hat dann die Form:
Beobachtungen haben wir mehr Gleichungen als
Unbekannte. In diesem Fall ist die Lösung durch Ausgleichsrechnung zu
erhalten. Dazu ist das Gleichungssystem in das entsprechende System von
Normalgleichungen zu überführen. Die dazu erforderlichen Rechenschritte
lassen sich am einfachsten erläutern, aber auch für das Abarbeiten im
Computer am übersichtlichsten darstellen, wenn man zur Matritzenschreibweise
übergeht.
Gl. (17) hat dann die Form:
 |
(18) |
Der Anschaulichkeit halber schreiben wir dieses Gleichungssystem noch
einmal vollständig auf:
![\begin{displaymath}
\left[ \begin{array}{cccccccccc}
\alpha _{1} & 0 & 0 & \be...
...E_{\rm y,n} \\ E_{\rm z,n} \\
\end{array} \right]_{\bf\, .}
\end{displaymath}](img1149.png) |
(19) |
Das zu lösende System der Normalgleichungen erhalten wir aus Gl. (18)
durch Multiplikation von links mit der transponierten Matrix
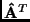 (der an der Hauptdiagonalen gespiegelten Matrix
(der an der Hauptdiagonalen gespiegelten Matrix 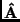 ):
):
 |
(20) |
Die linke Seite stellt jetzt die Koeffizientenmatrix des zu lösenden
Systems der Normalgleichungen dar.
Mit dem Ansatz
 |
(21) |
d.h. der Annahme einer in erster Näherung geradlinigen und gleichförmigen
Bewegung, ist dann das Gleichungssystem (19) iterativ zu lösen. Wenn wir
jetzt noch für die Epoche 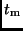 das Mittel aus den Beobachtungszeiten
das Mittel aus den Beobachtungszeiten
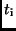 einführen,
einführen,
 |
(22) |
haben wir alle für die Berechnung der unbekannten Bahn notwendigen
Größen gegeben. Nach der ersten näherungsweisen Berechnung des
Gleichungssystems lassen sich aus dem jetzt bekannten Wert von
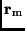 mittels der Reihenentwicklung (Gln. (15), (16)) neue verbesserte Werte
von
mittels der Reihenentwicklung (Gln. (15), (16)) neue verbesserte Werte
von
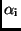 und
und
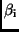 unter
Einbeziehung von Gliedern höherer Ordnung gewinnen.
Mit den neuen
unter
Einbeziehung von Gliedern höherer Ordnung gewinnen.
Mit den neuen
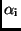 und
und
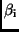 geht man dann wieder in das
Gleichungssystem ein und erhält verbesserte Werte für die
Integrationskonstanten der unbekannten Bahn in der Form der Komponenten
von
geht man dann wieder in das
Gleichungssystem ein und erhält verbesserte Werte für die
Integrationskonstanten der unbekannten Bahn in der Form der Komponenten
von
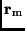 und
und
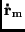 . Diesen Iterationsprozeß
setzt man so lange fort, bis sich die
. Diesen Iterationsprozeß
setzt man so lange fort, bis sich die
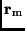 und
und
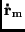 im Rahmen
der durch die Beobachtungen
im Rahmen
der durch die Beobachtungen
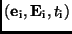 vorgegebenen
Genauigkeit nicht mehr ändern.
Das hier beschriebene Verfahren wird immer dann gute Ergebnisse liefern,
wenn die Zeitdifferenzen
vorgegebenen
Genauigkeit nicht mehr ändern.
Das hier beschriebene Verfahren wird immer dann gute Ergebnisse liefern,
wenn die Zeitdifferenzen
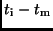 klein gegen die Umlaufzeit
klein gegen die Umlaufzeit
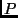 des
Himmelskörpers sind, da dann die Reihenentwicklung (Gl.(13)) schnell
konvergiert. Liegen größere Zeitabstände zwischen den Beobachtungen
vor, so ist es im Sinne einer raschen Konvergenz besser, die geschlossenen
Ausdrücke für die
des
Himmelskörpers sind, da dann die Reihenentwicklung (Gl.(13)) schnell
konvergiert. Liegen größere Zeitabstände zwischen den Beobachtungen
vor, so ist es im Sinne einer raschen Konvergenz besser, die geschlossenen
Ausdrücke für die
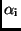 und
und
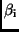 zu verwenden. Diese
lassen
sich mit Hilfe der Konstanz des Drehimpulses
zu verwenden. Diese
lassen
sich mit Hilfe der Konstanz des Drehimpulses 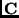 unter Ausnutzung
des Flächensatzes,
unter Ausnutzung
des Flächensatzes,
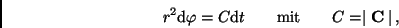 |
(23) |
ableiten und ergeben sich zu
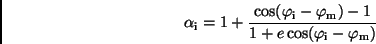 |
(24) |
und
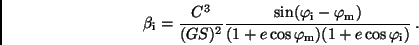 |
(25) |
Unter Anwendung des Flächensatzes lassen sich aus den bekannten
Zeitdifferenzen
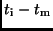 auch die Differenzen der wahren Anomalien
auch die Differenzen der wahren Anomalien
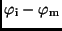 berechnen, die man in diesem Fall zur Berechnung der
berechnen, die man in diesem Fall zur Berechnung der
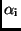 und
und
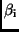 benötigt. Einsetzen für
benötigt. Einsetzen für 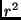 in den Flächensatz gibt:
in den Flächensatz gibt:
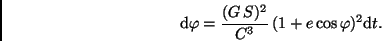 |
(26) |
Durch Anwendung eines numerischen Integrationsverfahrens lassen sich aus
Gl. (26) und der bekannten Anomalie
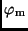 zur Epoche
zur Epoche 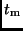 die wahren Anomalien
die wahren Anomalien
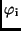 zu den Zeiten
zu den Zeiten 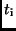 berechnen.
Als häufig benutztes Verfahren bietet sich das Runge-Kutta-Verfahren
an. Wählt man als Schrittweite
berechnen.
Als häufig benutztes Verfahren bietet sich das Runge-Kutta-Verfahren
an. Wählt man als Schrittweite
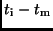 , so erhält man:
, so erhält man:
und schließlich
.
\end{displaymath}](img1166.png) |
(27) |
Im allgemeinen wird man ein großes Zeitintervall
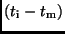 noch einmal
in
noch einmal
in 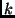 kleinere Intervalle
kleinere Intervalle 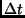 zerlegen
zerlegen
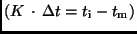 ,
um ein möglichst genaues Resultat für
,
um ein möglichst genaues Resultat für
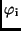 zu erhalten.
Die wahre Anomalie
zu erhalten.
Die wahre Anomalie
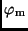 zum Zeitpunkt
zum Zeitpunkt 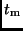 ergibt sich
als Winkel
zwischen dem Ortsvektor
ergibt sich
als Winkel
zwischen dem Ortsvektor
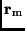 und dem LAPLACEvektor
und dem LAPLACEvektor 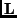 :
:
 |
(28) |
Eine ausführliche Darstellung der Bahnbestimmung nach der hier
vorgestellten Methode findet sich in [1] und [2].
Für die praktische Rechnung wird der für die Bewegung der Planeten
maßgebliche Parameter, das Produkt
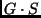 , im astronomischen Einheitensystem ausgedrückt [3]. Dabei ist die
Masseneinheit die Sonnenmasse
, im astronomischen Einheitensystem ausgedrückt [3]. Dabei ist die
Masseneinheit die Sonnenmasse 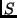 , die Zeiteinheit der Tag
, die Zeiteinheit der Tag 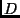 und die
Entfernungseinheit
und die
Entfernungseinheit
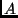 der Radius einer Kreisbahn, in der ein masseloser Körper die Sonne
(die Masseneinheit) in
der Radius einer Kreisbahn, in der ein masseloser Körper die Sonne
(die Masseneinheit) in 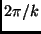 Tagen umrunden würde. Die große Halbachse
Tagen umrunden würde. Die große Halbachse
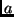 der Erdbahn ist mit dieser Definition
der Erdbahn ist mit dieser Definition
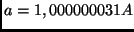 .
. 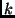 ist die
GAUSSsche Gravitationskonstante und hat den Zahlenwert
ist die
GAUSSsche Gravitationskonstante und hat den Zahlenwert
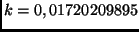 .
Im astronomischen Einheitensystem gilt also:
.
Im astronomischen Einheitensystem gilt also:
 |
(29) |




Next: Reduktion der Beobachtungen
Up: Grundlagen
Previous: Physikalische und geometrische Eigenschaften
Contents
Juergen Weiprecht
2002-10-29

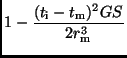
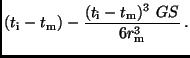
![\begin{displaymath}
\left[ \begin{array}{cccccccccc}
\alpha _{1} & 0 & 0 & \be...
...E_{\rm y,n} \\ E_{\rm z,n} \\
\end{array} \right]_{\bf\, .}
\end{displaymath}](img1149.png)

![\begin{eqnarray*}
K_1 & = & \frac{(G\,S)^2}{C^3}(1+e \cos \varphi_{\rm m})^2, \...
...C^3}[1+e \cos (\varphi_{\rm m} +K_3\,(t_{\rm i}
-t_{\rm m})]^2
\end{eqnarray*}](img1165.png)