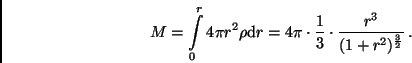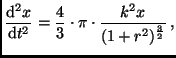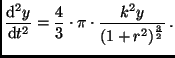Next: Zentralkräfte, die Potenzen des
Up: Das allgemeine Keplerproblem
Previous: Das allgemeine Keplerproblem
Contents
Durch Sternzählungen in Kugelsternhaufen erhält man bei geeigneter
Wahl der Einheiten und der Normierungsbedingung, daß die Sterndichte 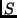 im Zentrum des Haufens gleich Eins ist:
im Zentrum des Haufens gleich Eins ist:
 |
(7) |
Jeder Einzelstern wird sich ständig unter dem Einfluß der Gesamtmasse
der übrigen Sterne befinden. Die individuellen Anziehungskräfte werden
nur dann eine Rolle spielen, wenn im Verlauf der Bewegung
zwei Sterne einander sehr nahe kommen. Dieses Problem wollen wir
hier vernachlässigen. Wir haben es hier also in erster Näherung nicht
mit einem Störungsproblem [1], sondern mit einer andersartigen
Zentralkraft zu tun.
Da die Massen von Hauptreihensternen nur
etwa um den Faktor 30 verschieden sind und ein Kugelsternhaufen
im Durchschnitt 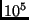 Sterne enthält, können wir für die Sternmasse
mit einem mittleren Wert rechnen. Wenn die Sterne verschiedener Massen
nicht unterschiedlich stark gegen das Zentrum des Haufens konzentriert
sind, wird man dabei keinen wesentlichen Fehler machen. Wir können
also in guter Näherung die Sterndichte
Sterne enthält, können wir für die Sternmasse
mit einem mittleren Wert rechnen. Wenn die Sterne verschiedener Massen
nicht unterschiedlich stark gegen das Zentrum des Haufens konzentriert
sind, wird man dabei keinen wesentlichen Fehler machen. Wir können
also in guter Näherung die Sterndichte 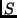 gleich der Massendichte
gleich der Massendichte 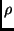 setzen. Auf unseren Probekörper mit der Masse
setzen. Auf unseren Probekörper mit der Masse 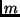 wirkt die gesamte
Masse
wirkt die gesamte
Masse 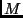 innerhalb des Radius
innerhalb des Radius 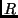 , der kleiner als der Abstand
, der kleiner als der Abstand 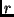 des Probekörpers ist, so, als wäre diese Masse bei
des Probekörpers ist, so, als wäre diese Masse bei 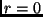 im Mittelpunkt
des Haufens konzentriert. Die Wirkungen der Massen außerhalb von
im Mittelpunkt
des Haufens konzentriert. Die Wirkungen der Massen außerhalb von 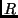 auf
auf 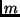 heben sich gegenseitig auf. Man erhält die Masse innerhalb
von
heben sich gegenseitig auf. Man erhält die Masse innerhalb
von 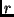 durch Integration über die Massendichte:
durch Integration über die Massendichte:
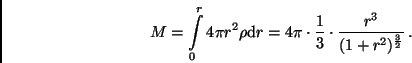 |
(8) |
Die Kraft auf den Probekörper 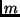 ergibt sich dann einfach zu:
ergibt sich dann einfach zu:
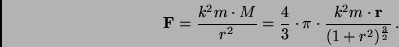 |
(9) |
Die Differentialgleichungen für die Bewegung des Probekörpers im
Kugelsternhaufen lauten:
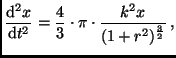 |
|
|
|
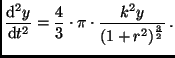 |
|
|
(10) |
Jede dieser Gleichungen läßt sich in zwei Differentialgleichungen
1. Ordnung zerlegen, die man dann z.B. mit einem Runge-Kutta-Verfahren
integrieren kann (siehe Aufgabe 13 und [6]).
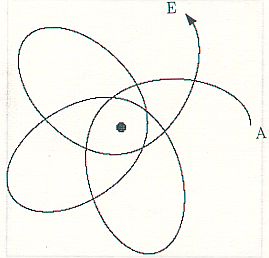
Als Bahnform erhält man ellipsenähnliche Kurven mit sich drehender
Apsidenlinie. Ein Beispiel ist in Abb. 2 dargestellt.




Next: Zentralkräfte, die Potenzen des
Up: Das allgemeine Keplerproblem
Previous: Das allgemeine Keplerproblem
Contents
Juergen Weiprecht
2002-10-29