



Next: Bibliography
Up: Interpolation in Tafeln
Previous: Lineare Interpolation
Contents
Reicht die durch lineare Interpolation gewonnene Annäherung von 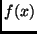 durch
durch
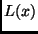 nicht aus, so wählt man als Näherungsfunktion ein Polynom 2. Grades und
spricht dann von einer quadratischen Interpolation. Zu ihrer Darstellung werden
3 Tafelwerte benötigt. Diese können bezüglich
nicht aus, so wählt man als Näherungsfunktion ein Polynom 2. Grades und
spricht dann von einer quadratischen Interpolation. Zu ihrer Darstellung werden
3 Tafelwerte benötigt. Diese können bezüglich 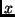 unterschiedlich angeordnet
sein. Relativ geringe Fehler ergeben sich, wenn
unterschiedlich angeordnet
sein. Relativ geringe Fehler ergeben sich, wenn 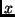 im Intervall
im Intervall
liegt, und man zur Darstellung der quadratischen Näherungsfunktion 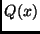 die
Funktionswerte
die
Funktionswerte
benutzt. Dabei ist eine äquidistante Lage der Argumente vorausgesetzt. Mit
ihnen berechnet sich der Näherungswert zu
(STIRLINGsche Interpolationsformel).
Juergen Weiprecht
2021-04-08