



Next: Messung und Meßverfahren
Up: Grundlagen
Previous: Zusammenhang zwischen den geographischen
Contents
3.1.2 Meridiandurchgang, Kulmination und scheinbare Bahnkurve der
Sonne
Um eine höhere Genauigkeit bei der geographischen Ortsbestimmung zu
erreichen, beobachtet man die Sonne
nicht allein bei ihrer Kulmination, sondern ermittelt die Höhen 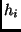 (wobei die Höhenabweichungen infolge von Refraktion und täglicher
Parallaxe bereits korrigiert worden sind)
bei unterschiedlichen mittleren Sonnenzeiten
(wobei die Höhenabweichungen infolge von Refraktion und täglicher
Parallaxe bereits korrigiert worden sind)
bei unterschiedlichen mittleren Sonnenzeiten 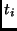 entlang der scheinbaren täglichen Bahn der Sonne
in der Nähe ihres Kulminationspunktes (davor und danach).
Durch die so erhaltenen Meßpunkte mit den Koordinaten
entlang der scheinbaren täglichen Bahn der Sonne
in der Nähe ihres Kulminationspunktes (davor und danach).
Durch die so erhaltenen Meßpunkte mit den Koordinaten 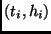 wird
eine die scheinbare tägliche Bahnkurve annähernde Ausgleichskurve
gelegt, aus deren Verlauf
wird
eine die scheinbare tägliche Bahnkurve annähernde Ausgleichskurve
gelegt, aus deren Verlauf 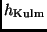 wie auch die Kulminationszeit
wie auch die Kulminationszeit
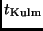 bestimmt werden können
(Formalismus folgt weiter unten).
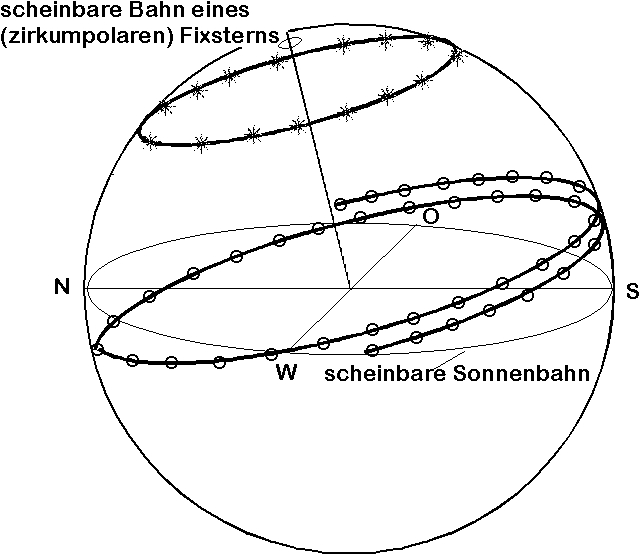
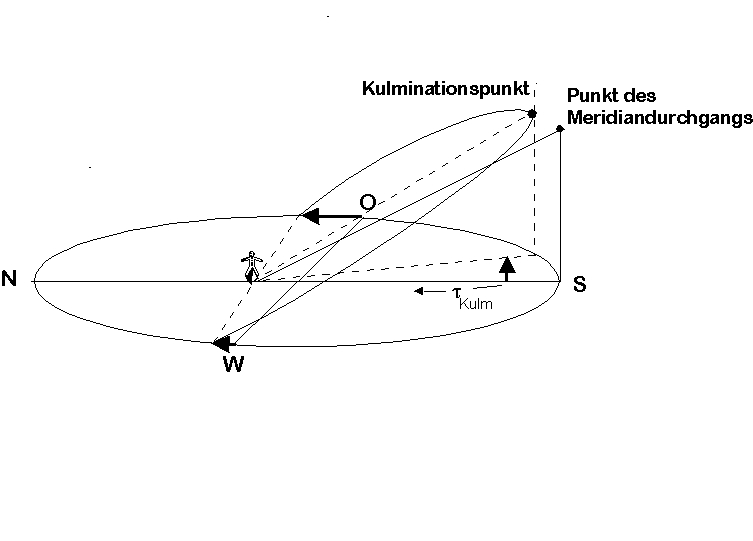
Während ihrer scheinbaren täglichen Bewegung erreichen die Gestirne
südlich des Himmelsnordpols ihre größte Höhe über dem Horizont
(obere Kulmination, siehe Abb. 3). Für Objekte mit
bestimmt werden können
(Formalismus folgt weiter unten).
Während ihrer scheinbaren täglichen Bewegung erreichen die Gestirne
südlich des Himmelsnordpols ihre größte Höhe über dem Horizont
(obere Kulmination, siehe Abb. 3). Für Objekte mit
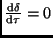 (
(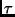 im Sinne einer Zeit), d.h.
für Fixsterne, stimmt die für die geographische Längenbestimmung
gesuchte Zeit des Meridiandurchganges mit der
der oberen Kulmination überein.
Die Sonne erreicht ihre gr"o"ste H"ohe an den meisten Tagen des Jahres
nicht genau im Meridian, da f"ur sie meist
im Sinne einer Zeit), d.h.
für Fixsterne, stimmt die für die geographische Längenbestimmung
gesuchte Zeit des Meridiandurchganges mit der
der oberen Kulmination überein.
Die Sonne erreicht ihre gr"o"ste H"ohe an den meisten Tagen des Jahres
nicht genau im Meridian, da f"ur sie meist
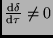 gilt
(siehe Abb. 3).
gilt
(siehe Abb. 3).
Für die Bestimmung der geographischen Länge auf Grundlage von
Sonnenbeobachtungen benötigt man eine Beziehung,
die es gestattet, aus der zeitlichen Änderung der Deklination
der Sonne
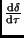 und der ungefähren
geographischen Breite
des Beobachtungsortes (bei unterschiedlichen Breiten sind die Ebenen der
Tagbögen der Gestirne verschieden steil zur Horizontebene geneigt) den
Stundenwinkel
und der ungefähren
geographischen Breite
des Beobachtungsortes (bei unterschiedlichen Breiten sind die Ebenen der
Tagbögen der Gestirne verschieden steil zur Horizontebene geneigt) den
Stundenwinkel
 zu berechnen und so auf die Zeit des
Meridiandurchganges
zu berechnen und so auf die Zeit des
Meridiandurchganges
 (
(
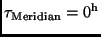 )
zu schließen. Grundlage zur Herleitung dieser Beziehung ist diejenige
der in Aufgabe "`Aufsuchen und Klassifizieren astronomischer
Beobachtungsobjekte"' gegebenen Umrechnungsformeln von äquatorialen in
horizontale Koordinaten, welche die Azimutkoordinate nicht enthält.
Differenziert man diese nach der Zeit (
)
zu schließen. Grundlage zur Herleitung dieser Beziehung ist diejenige
der in Aufgabe "`Aufsuchen und Klassifizieren astronomischer
Beobachtungsobjekte"' gegebenen Umrechnungsformeln von äquatorialen in
horizontale Koordinaten, welche die Azimutkoordinate nicht enthält.
Differenziert man diese nach der Zeit (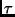 ) und
setzt
) und
setzt
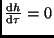 (zur Kulmination verschwindet die
Höhenänderung), so ergibt sich bei
(zur Kulmination verschwindet die
Höhenänderung), so ergibt sich bei
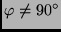 für den Stundenwinkel der
Kulmination
für den Stundenwinkel der
Kulmination
wobei alle Winkel im Bogenmaß ausgedrückt sein sollen. Für kleine Winkel
 gilt dann:
gilt dann:
 und
und
 , so daß man erhält:
, so daß man erhält:
In Winkelsekunden ausgedrückt ergibt sich für
 :
:
Die tägliche Deklinationsänderung kann mit Hilfe der aus astronomischen
Jahrbüchern entnehmbaren Sonnendeklinationen interpoliert werden.
Diese soll mit 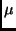 bezeichnet
werden. Zwischen
bezeichnet
werden. Zwischen 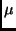 (Einheit [
(Einheit [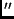 /d]) und
/d]) und
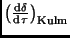 (Einheit Bogenmaß bzw. [
(Einheit Bogenmaß bzw. [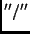 ]) besteht folgender Zusammmenhang:
]) besteht folgender Zusammmenhang:
Die gesuchte Zeitdifferenz (mittlere Sonnenzeit) zwischen Meridiandurchgang
und Kulmination
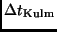 ergibt sich nach
Umrechnung der Winkelsekunden in Zeitsekunden (1
ergibt sich nach
Umrechnung der Winkelsekunden in Zeitsekunden (1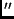 entspricht
entspricht 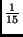 s)
und Umwandlung von Sternzeitmaß in das Zeitmaß der mittleren Sonne
(
s)
und Umwandlung von Sternzeitmaß in das Zeitmaß der mittleren Sonne
(
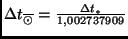 ):
):
Abschließend soll die
scheinbare tägliche Bahnkurve der Sonne in der
Nähe ihrer Kulmination näherungsweise durch eine Funktion
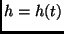 beschrieben werden.
Die Form der
scheinbaren täglichen Bahnkurve der Sonne
erscheint für den Beobachtungszeitraum
von ca. 2 h im Vergleich zu der eines Fixsterns nur gering
verändert (die verschobene Lage des Kulminationspunktes
hingegen ist beachtenswert).
Die Bestimmung einer einfachen Näherungsfunktion
beschrieben werden.
Die Form der
scheinbaren täglichen Bahnkurve der Sonne
erscheint für den Beobachtungszeitraum
von ca. 2 h im Vergleich zu der eines Fixsterns nur gering
verändert (die verschobene Lage des Kulminationspunktes
hingegen ist beachtenswert).
Die Bestimmung einer einfachen Näherungsfunktion 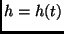 für die scheinbare tägliche Bahnkurve eines Fixsterns geht vom
exakten Zusammenhang zwischen der Höhe und den äquatorialen Koordinaten
aus (siehe Aufgabe "`Aufsuchen und Klassifizieren astronomischer
Beobachtungsobjekte"', dabei erscheint zunächst anstatt der
mittleren Sonnenzeit
für die scheinbare tägliche Bahnkurve eines Fixsterns geht vom
exakten Zusammenhang zwischen der Höhe und den äquatorialen Koordinaten
aus (siehe Aufgabe "`Aufsuchen und Klassifizieren astronomischer
Beobachtungsobjekte"', dabei erscheint zunächst anstatt der
mittleren Sonnenzeit 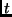 der im Sternzeitmaß gemessene Stundenwinkel
der im Sternzeitmaß gemessene Stundenwinkel
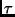 ), der nach
), der nach 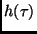 umgestellt
wie folgt aussieht:
umgestellt
wie folgt aussieht:
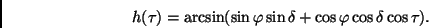 |
(5) |
Durch eine Taylor-Entwicklung in der Nähe des Stundenwinkels der
Kulmination
 erhält man
erhält man
Für Beobachtungen nach der Kulmination setzt man
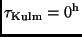 , für Beobachtungen vor der Kulmination
, für Beobachtungen vor der Kulmination
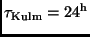 .
Wegen
.
Wegen 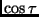 in (5) werden die Terme mit den ungeradzahligen
Ableitungen zu Null, und es ergibt sich für
in (5) werden die Terme mit den ungeradzahligen
Ableitungen zu Null, und es ergibt sich für 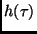 ein nur aus
Parabelfunktionen bestehendes Polynom. Dieses kann in erster Näherung
bereits nach dem quadratischen Glied abgebrochen werden, so daß sich
mit
ein nur aus
Parabelfunktionen bestehendes Polynom. Dieses kann in erster Näherung
bereits nach dem quadratischen Glied abgebrochen werden, so daß sich
mit
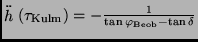 der folgende Ausdruck für die Ausgleichskurve
der folgende Ausdruck für die Ausgleichskurve 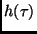 ergibt
(
ergibt
(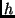 und
und 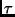 im Bogenmaß):
im Bogenmaß):
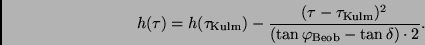 |
(6) |
Setzt man in (6) 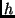 und
und 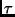 in
in ![$[^\circ]$](img372.png) ein,
überführt
ein,
überführt 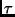 vom Gradmaß ins Zeitmaß (1
vom Gradmaß ins Zeitmaß (1
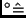 4min) und
transformiert
4min) und
transformiert 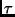 abschließend in die mittlere Sonnenzeit
abschließend in die mittlere Sonnenzeit
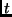 in [min] (Faktor 1,002737909), so erhält man:
in [min] (Faktor 1,002737909), so erhält man:




Next: Messung und Meßverfahren
Up: Grundlagen
Previous: Zusammenhang zwischen den geographischen
Contents
Juergen Weiprecht
2002-10-29

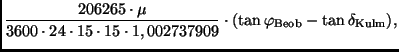
![$\displaystyle \frac{\mu}{94,5} \cdot (\tan \varphi_{\rm Beob} - \tan
\delta_{\r...
...\ \ \ \ \ \qquad \qquad [\Delta t_{\rm Kulm}/{\rm s}, \
\mu/\frac{''}{\rm d}].$](img362.png)
![$\displaystyle h(t) \frac{[^\circ]}{\frac{180^\circ}{\pi}}$](img374.png)
![$\displaystyle h(t_{\rm Kulm})
\frac{[^\circ]}{\frac{180^\circ}{\pi}} \ - \
\fr...
... 2 \cdot (\frac{180^\circ}{\pi})^2 \cdot (4{\rm min})^2 \cdot
(1,002737909)^2},$](img375.png)
![$\displaystyle h(t_{\rm Kulm}) \ - \
\frac{(t - t_{\rm Kulm} )^2}
{(\tan \varphi_{\rm Beob} - \tan \delta) \cdot 1823}; \qquad \qquad
[h/^{\circ}, t/{\rm min}].$](img377.png)