



Next: Analyse der Beobachtungen
Up: Grundlagen
Previous: Formen der Lichtkurven
Contents
Die relative Bahn einer Komponente eines Doppelsternsystems
um die als Koordinatenursprung dienende Hauptkomponente kann durch
die gleichen Parameter wie im Fall der Bahnen von Körpern unseres
Sonnensystems beschrieben werden. Lediglich die Bezugsebene ist,
angepaßt an die unterschiedliche Art der Beobachtung, anders definiert. Die
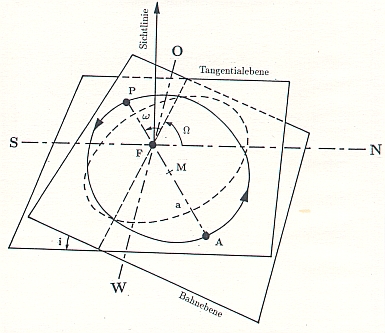
anschließend aufgeführten Bahnelemente sind in Abb. 5 dargestellt.
- a:
- Die große Halbachse der relativen Bahn der Komponente B
um A. Dabei ist
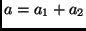 und
und 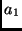 ,
, 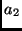 sind
die großen Halbachsen der Bahnen beider Körper um den
Schwerpunkt des Systems.
sind
die großen Halbachsen der Bahnen beider Körper um den
Schwerpunkt des Systems.
- e:
- Die numerische Exzentrizität der Bahn.
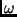 :
:- Der Winkelabstand des Periastrons vom
aufsteigenden
Knoten, gemessen in der Bahnebene und in der
Bewegungsrichtung des Begleiters.
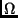 :
:- Die Länge des aufsteigenden Knotens der Bahn.
Sie wird
gemessen in der Tangentialebene an die scheinbare
Himmelskugel durch den Stern A, ausgehend von der
Nordrichtung, und ist immer kleiner als
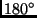 . Die
Knoten sind die Durchstoßpunkte der wahren Bahn
durch die Tangentialebene. Aufsteigend bedeutet
dabei, daß der Stern sich auf den Beobachter
zubewegt.
. Die
Knoten sind die Durchstoßpunkte der wahren Bahn
durch die Tangentialebene. Aufsteigend bedeutet
dabei, daß der Stern sich auf den Beobachter
zubewegt.
- i:
- Die Neigung der wahren Bahn bezüglich der
Tangentialebene.
- U:
- Die Umlaufperiode. Hierzu muß bemerkt werden,
daß alle in Katalogen aufgelisteten oder von
Beobachtern in irgendeiner Weise gegebenen Perioden
nur scheinbare Perioden
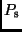 sind, die sich auf ein
heliozentrisches Koordinatensystem beziehen. Als Folge
der endlichen Ausbreitungsgeschwindigkeit des Lichts
ergibt sich die wahre Periode
sind, die sich auf ein
heliozentrisches Koordinatensystem beziehen. Als Folge
der endlichen Ausbreitungsgeschwindigkeit des Lichts
ergibt sich die wahre Periode 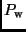 bezogen auf den
Schwerpunkt des Doppelsternsystems wie folgt:
bezogen auf den
Schwerpunkt des Doppelsternsystems wie folgt:
 |
(5) |
Hier bedeuten 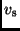 die heliozentrische
Radialgeschwindigkeit des Schwerpunkts und c die
Lichtgeschwindigkeit.
die heliozentrische
Radialgeschwindigkeit des Schwerpunkts und c die
Lichtgeschwindigkeit.
- T:
- Die Zeit (Epoche) des Durchgangs des Begleiters
durch das Periastron.
 |
 |
Bei den Doppelsternbahnen wird ein Bahnelement mehr benötigt
als im Fall der Bahnbestimmung eines Körpers im Sonnensystem.
Da die Massen beider Komponenten eine vergleichbare Größe haben,
tritt die Masensumme als zusätzlicher Parameter auf (siehe Gl. 2).
Während im Sonnensystem die Angabe von 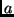 ausreicht und
ausreicht und 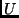 damit über das
dritte KEPLERsche Gesetz bestimmt ist, muß im Fall von Doppelsternbahnen
die Umlaufzeit
damit über das
dritte KEPLERsche Gesetz bestimmt ist, muß im Fall von Doppelsternbahnen
die Umlaufzeit 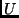 unabhängig bestimmt werden.
Zusätzlich zu den Bahnelementen müssen aus der Lichtkurve noch
die individuellen Parameter der einzelnen Komponenten bestimmt werden.
Diese Zustandsgrößen der Sterne zusammen mit den Bahnelementen liefern
erst eine vollständige Beschreibung des Systems. Die zu bestimmenden
Größen für die beiden Komponente sind: die Radien
unabhängig bestimmt werden.
Zusätzlich zu den Bahnelementen müssen aus der Lichtkurve noch
die individuellen Parameter der einzelnen Komponenten bestimmt werden.
Diese Zustandsgrößen der Sterne zusammen mit den Bahnelementen liefern
erst eine vollständige Beschreibung des Systems. Die zu bestimmenden
Größen für die beiden Komponente sind: die Radien 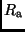 und
und 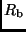 ,
die Massen
,
die Massen 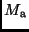 und
und 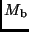 , die Leuchtkräfte
, die Leuchtkräfte 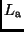 und
und
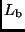 , die effektiven Temperaturen
, die effektiven Temperaturen 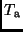 und
und 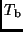 , die
Flächenhelligkeiten
, die
Flächenhelligkeiten 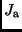 und
und 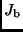 sowie der Grad der
Randverdunklung
sowie der Grad der
Randverdunklung
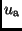 und
und 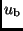 . Diese Parameter sind jedoch keine unabhängigen
Parameter. Für die Masse besteht sowohl eine Abhängigkeit über das
dritte KEPLERsche Gesetz (Gl. 2) mit
. Diese Parameter sind jedoch keine unabhängigen
Parameter. Für die Masse besteht sowohl eine Abhängigkeit über das
dritte KEPLERsche Gesetz (Gl. 2) mit 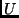 und
und 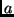 als auch mit der
Leuchtkraft über die Masse-Leuchtkraft-Beziehung,
als auch mit der
Leuchtkraft über die Masse-Leuchtkraft-Beziehung,
 |
(6) |
Ebenso sind Radius, Temperatur und Leuchtkraft über
 |
(7) |
verknüpft und die beobachteten Helligkeiten 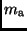 und
und 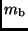 sind mit
den Leuchtkräften durch
sind mit
den Leuchtkräften durch
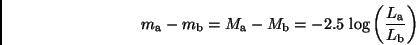 |
(8) |
verbunden, da für einen Beobachter auf der Erde beide Komponenten
nahezu die gleiche Entfernung haben.
Um das Problem der Randverdunklung möglichst einfach lösen zu können,
nehmen wir an, daß die Flächenhelligkeit zum Sternrand hin
proportional zum Kosinus des Winkels zwischen der Sichtlinie zum
Beobachter und der Normalen zum betrachteten Flächenelement ist.
 |
(9) |
Das gilt nur unter der Voraussetzung einer grauen Atmosphäre und
der EDDINGTONschen Näherung (siehe Aufgabe Nr. 12 Gl. 17).
Der Grad der Randverdunklung wird durch 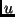 angegeben, wobei
angegeben, wobei
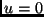 konstante Flächenhelligkeit bedeutet. Im Fall
konstante Flächenhelligkeit bedeutet. Im Fall 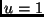 fällt die Flächenhelligkeit zum Rand auf Null ab. Die Auswirkungen
der Randverdunklung auf die Form der Bedeckungslichtkurve während
eines Minimums sind in Abb. 6. dargestellt.
Wir haben jetzt alle Größen, mit denen wir die Beobachtungen
vollständig beschreiben können, kennengelernt und können uns jetzt
mit der Analyse der Beobachtungen beschäftigen.
fällt die Flächenhelligkeit zum Rand auf Null ab. Die Auswirkungen
der Randverdunklung auf die Form der Bedeckungslichtkurve während
eines Minimums sind in Abb. 6. dargestellt.
Wir haben jetzt alle Größen, mit denen wir die Beobachtungen
vollständig beschreiben können, kennengelernt und können uns jetzt
mit der Analyse der Beobachtungen beschäftigen.




Next: Analyse der Beobachtungen
Up: Grundlagen
Previous: Formen der Lichtkurven
Contents
Juergen Weiprecht
2002-10-29