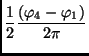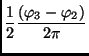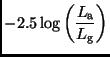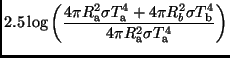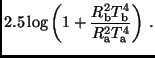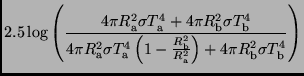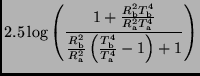Next: Versuchsanleitung
Up: Analyse der Beobachtungen
Previous: Spektroskopische Beobachtungen - Die
Contents
Die beobachtete Lichtkurve eines Veränderlichen besteht aus einer
Serie diskreter Messungen der Helligkeit des Objekts zu definierten
Zeitpunkten. Die Helligkeit wird dabei generell in Größenklassen
 |
(14) |
ausgedrückt. Dabei ist 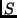 der Strahlungsstrom, der uns vom Stern erreicht
in [J
der Strahlungsstrom, der uns vom Stern erreicht
in [J 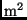
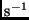 ] und
] und 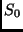 ein fiktiver
Strahlungsstrom, der der Helligkeit
ein fiktiver
Strahlungsstrom, der der Helligkeit 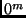 entspricht
(siehe Aufgabe Nr. 8 Gl. 1).
Für den Fall der Bedeckungsveränderlichen (beide Sterne sind
gleich weit vom Beobachter entfernt) kann man
entspricht
(siehe Aufgabe Nr. 8 Gl. 1).
Für den Fall der Bedeckungsveränderlichen (beide Sterne sind
gleich weit vom Beobachter entfernt) kann man 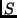 auch durch den
Gesamtstrahlungsstrom, der von der Sternoberfläche ausgeht - die
Leuchtkraft des Sterns,
auch durch den
Gesamtstrahlungsstrom, der von der Sternoberfläche ausgeht - die
Leuchtkraft des Sterns, 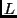 - ersetzen.
Beträgt die Umlaufperiode
- ersetzen.
Beträgt die Umlaufperiode 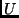 Tage, kommt es während
eines Umlaufs, bei einer nicht zu starken Neigung der Bahn
gegen die Sichtlinie, normalerweise zu zwei Bedeckungen. Für gewöhnlich
bewirkt eine Bedeckung, die Hauptbedeckung, einen tieferen Einschnitt in
die Lichtkurve als die andere, die sekundäre Bedeckung. Kennt man den
zeitlichen Abstand zwischen zwei Hauptminima, der gleich der
Periode
Tage, kommt es während
eines Umlaufs, bei einer nicht zu starken Neigung der Bahn
gegen die Sichtlinie, normalerweise zu zwei Bedeckungen. Für gewöhnlich
bewirkt eine Bedeckung, die Hauptbedeckung, einen tieferen Einschnitt in
die Lichtkurve als die andere, die sekundäre Bedeckung. Kennt man den
zeitlichen Abstand zwischen zwei Hauptminima, der gleich der
Periode 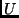 des Bedeckungsveränderlichen ist, und bezeichnet man den
Zeitpunkt des primären Minimums mit
des Bedeckungsveränderlichen ist, und bezeichnet man den
Zeitpunkt des primären Minimums mit 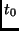 , so lassen sich viele
in ungleichmäßigen Zeitabständen
, so lassen sich viele
in ungleichmäßigen Zeitabständen 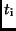 gewonnene Beobachtungen der
Lichtkurve in einer gemeinsamen, auf den Phasenwinkel
gewonnene Beobachtungen der
Lichtkurve in einer gemeinsamen, auf den Phasenwinkel 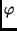 ,
,
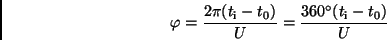 |
(15) |
bezogenen Darstellung (siehe Abb. 9), auftragen.
Ein weiterer Vorteil dieser Darstellung ergibt sich aus der Tatsache,
daß der Phasenwinkel 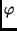 gleich der mittleren Anomalie der
relativen Bahn der lichtschwächeren Komponente ist.
Eine erste Klassifikation der Lichtkurve erfolgt nach dem Gesamteindruck,
d.h. den im Abschnitt "`Formen der Lichtkurve"' genannten Kriterien.
Im weiteren beschäftigen wir uns ausschließlich mit der Analyse der
Lichtkurve von Algol-Systemen. Massenaustausch und Verformung der Sterne
spielen also keine Rolle. Die Lichtkurve ist durch die geometrischen
Eigenschaften bestimmt und kann durch Randverdunklung und Reflexion
beeinflußt werden (siehe auch C. HOFFMEISTER [3]).
Außerhalb der Minima ist die Lichtkurve konstant. Man beobachtet das
Gesamtlicht beider Komponenten. Der Gesamtstrahlungsstrom ergibt sich
aus der Summe der Strahlungsströme der Komponenten:
gleich der mittleren Anomalie der
relativen Bahn der lichtschwächeren Komponente ist.
Eine erste Klassifikation der Lichtkurve erfolgt nach dem Gesamteindruck,
d.h. den im Abschnitt "`Formen der Lichtkurve"' genannten Kriterien.
Im weiteren beschäftigen wir uns ausschließlich mit der Analyse der
Lichtkurve von Algol-Systemen. Massenaustausch und Verformung der Sterne
spielen also keine Rolle. Die Lichtkurve ist durch die geometrischen
Eigenschaften bestimmt und kann durch Randverdunklung und Reflexion
beeinflußt werden (siehe auch C. HOFFMEISTER [3]).
Außerhalb der Minima ist die Lichtkurve konstant. Man beobachtet das
Gesamtlicht beider Komponenten. Der Gesamtstrahlungsstrom ergibt sich
aus der Summe der Strahlungsströme der Komponenten:
 |
(16) |
Die Gesamthelligkeit 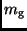 berechnet sich dann wie folgt:
berechnet sich dann wie folgt:
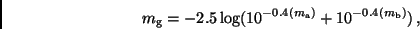 |
(17) |
Bei den Minima sind zwei unterschiedliche Erscheinungen möglich.
Steht der größere Stern mit dem Strahlungsstrom 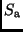 vollständig
vor der kleineren Komponente, handelt es sich um eine Bedeckung
(englisch = eclipse), und der
Gesamtstrahlungsstrom
vollständig
vor der kleineren Komponente, handelt es sich um eine Bedeckung
(englisch = eclipse), und der
Gesamtstrahlungsstrom 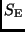 während der Zeitdauer der Totalität
ist gleich
während der Zeitdauer der Totalität
ist gleich 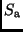 . Zieht der kleinere Stern mit dem Strahlungsstrom
. Zieht der kleinere Stern mit dem Strahlungsstrom
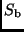 vor der Scheibe der
größeren Komponente vorüber, handelt es sich um einen Durchgang (Transit).
Der Gesamtstrahlungsstrom
vor der Scheibe der
größeren Komponente vorüber, handelt es sich um einen Durchgang (Transit).
Der Gesamtstrahlungsstrom 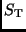 ergibt sich im Fall einer solchen
ringförmigen Finsternis zu:
ergibt sich im Fall einer solchen
ringförmigen Finsternis zu:
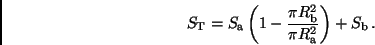 |
(18) |
Haben die Sterne unterschiedliche Radien, wechseln stets totale
und ringförmige Finsternisse einander ab.
In Abbildung 10 ist ein typisches Minimum für zwei Sterne mit
unterschiedlichen Radien dargestellt.
Im Fall eines Transits bedeckt der kleinere Stern zunächst die
randverdunkelten Zonen des größeren Sterns. Das bewirkt, daß während
der partiellen Phase der Abfall der Lichtkurve nicht geradlinig erfolgt.
Im Verlauf der ringförmigen Phase ist dann auch das Plateau, der untere
Teil der Lichtkurve, während des Minimums nicht mehr streng geradlinig
(siehe auch Abb. 6). Weicht die Neigung der Bahn gegen die Sichtlinie
merklich von 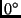 ab, kommt es nur noch zu partiellen Bedeckungen.
Das Plateau entartet zu einem Punkt. Dieser repräsentiert den Zeitpunkt
des Maximums der teilweisen Bedeckung. Das Minimum ist spitz wie im
Fall exakt gleich großer Sterne. Eine weitere Abweichung von der
schematisierten Lichtkurve kann sich durch den Reflexionseffekt ergeben.
Er tritt auf, wenn eine kleine, hellere und heiße Komponente einen
großen, lichtschwächeren und kühleren Stern umkreist. Kurz vor und
nach dem Nebenminimum (Transit) wird ein Teil des Lichts von der
Rückseite der heißen Komponente vom kühlen Stern in die Sichtlinie
reflektiert. Der kurz vor und nach dem Nebenminimum beobachtete
Strahlungsstrom ist also größer als der im Normallicht beobachtete
Gesamtstrahlungsstrom
ab, kommt es nur noch zu partiellen Bedeckungen.
Das Plateau entartet zu einem Punkt. Dieser repräsentiert den Zeitpunkt
des Maximums der teilweisen Bedeckung. Das Minimum ist spitz wie im
Fall exakt gleich großer Sterne. Eine weitere Abweichung von der
schematisierten Lichtkurve kann sich durch den Reflexionseffekt ergeben.
Er tritt auf, wenn eine kleine, hellere und heiße Komponente einen
großen, lichtschwächeren und kühleren Stern umkreist. Kurz vor und
nach dem Nebenminimum (Transit) wird ein Teil des Lichts von der
Rückseite der heißen Komponente vom kühlen Stern in die Sichtlinie
reflektiert. Der kurz vor und nach dem Nebenminimum beobachtete
Strahlungsstrom ist also größer als der im Normallicht beobachtete
Gesamtstrahlungsstrom 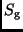 .
Hinsichtlich der Zustandsgrößen der Sterne lassen sich
aus der Analyse der Minima sowohl die Radien und die
effektiven Temperaturen der beiden Komponenten bestimmen. Das ist
besonders einfach im Fall einer näherungsweise oder exakt
kreisförmigen Bahn. Hier kann man aus den
Phasenwinkeln der Kontaktzeiten sofort die Radien der Sterne in Einheiten
der großen Halbachse (bzw. des Radius) der Bahn ableiten.
(siehe Abb. 10).
.
Hinsichtlich der Zustandsgrößen der Sterne lassen sich
aus der Analyse der Minima sowohl die Radien und die
effektiven Temperaturen der beiden Komponenten bestimmen. Das ist
besonders einfach im Fall einer näherungsweise oder exakt
kreisförmigen Bahn. Hier kann man aus den
Phasenwinkeln der Kontaktzeiten sofort die Radien der Sterne in Einheiten
der großen Halbachse (bzw. des Radius) der Bahn ableiten.
(siehe Abb. 10).
Zur Ableitung der effektiven Temperaturen ersetzen wir zunächst die
Strahlungsströme 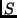 durch die Leuchtkräfte
durch die Leuchtkräfte 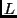 und betrachten die
Sterne näherungsweise als Schwarze Strahler.
Im Fall einer Bedeckung ergibt sich mit
und betrachten die
Sterne näherungsweise als Schwarze Strahler.
Im Fall einer Bedeckung ergibt sich mit
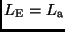 nach
Gln. 7,8,14 und 17
nach
Gln. 7,8,14 und 17
Unter Berücksichtigung von Gl. 19 ergibt sich ebenso einfach die
entsprechende Formel für einen Transit.
Jetzt wollen wir noch untersuchen, wie die Bahnelemente der Nebenkomponente
sich in Lage und Form der Minima widerspiegeln. Ist die Bahn exakt
kreisförmig, so folgen die Minima in genau 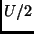 Tagen aufeinander.
Diese Aussage ist jedoch nicht umkehrbar eindeutig. Schaut man in der
Bahnebene genau entlang der großen Halbachse einer Bahn mit beliebiger
Exzentrizität, so folgen die Bedeckungen auch genau im Abstand von
Tagen aufeinander.
Diese Aussage ist jedoch nicht umkehrbar eindeutig. Schaut man in der
Bahnebene genau entlang der großen Halbachse einer Bahn mit beliebiger
Exzentrizität, so folgen die Bedeckungen auch genau im Abstand von 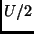 Tagen aufeinander. Infolge des 2. KEPLERschen Gesetzes (Drehimpulserhaltung)
ist aber die Geschwindigkeit der Komponente B im Apastron langsamer als im
Periastron. Die beiden Bedeckungen müssen sich also hinsichtlich ihrer
Zeitdauer unterscheiden. Benutzt man den Energiesatz für das
Zweikörperproblem in Form der Geschwindigkeitsbeziehung
Tagen aufeinander. Infolge des 2. KEPLERschen Gesetzes (Drehimpulserhaltung)
ist aber die Geschwindigkeit der Komponente B im Apastron langsamer als im
Periastron. Die beiden Bedeckungen müssen sich also hinsichtlich ihrer
Zeitdauer unterscheiden. Benutzt man den Energiesatz für das
Zweikörperproblem in Form der Geschwindigkeitsbeziehung
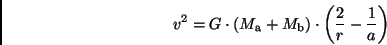 |
(22) |
und wendet sie für den Fall, daß die Sichtlinie parallel zur großen
Halbachse liegt, an, so kann man das Verhältnis der Geschwindigkeiten
im Periastron und im Apastron berechnen:
 |
(23) |
Da die Wege, die für eine vollständige Bedeckung zurückgelegt werden,
jeweils gleich sind, ist das Verhältnis der Zeiten der beiden
Minima ein Maß für die Exzentrizität der Bahn von B um A:
 |
(24) |
Sind jedoch die Intervalle zwischen den
Verfinsterungen nicht genau zeitgleich, so muß die Bahn exzentrisch
sein. Das Teilungsverhältnis, mit dem das Nebenminimum die Umlaufperiode
teilt, ist eine Funktion der Exzentrizität und des Winkels zwischen der
Sichtlinie und der Apsidenlinie. Bei engen, schnell rotierenden
Doppelsternsystemen kann es zu einer Drehung der Apsidenlinie kommen,
was sich in einer stetigen Änderung der Lage des Nebenminimums äußert.
Sowohl die gemessenen Radialgeschwindigkeiten als auch Zeitpunkte des
Eintritts der einzelnen Phasen werden durch die Bahnbewegung der Erde
um die Sonne periodisch verfälscht. Die Korrektur erhält man, indem man vom
geozentrischen zu einem heliozentrischen Koordinatensystem übergeht.
Die Beobachtungszeiten werden dann in heliozentrischer Zeit angegeben.
Dadurch wird die Zeitangabe unabhängig von der jahreszeitlich
unterschiedlichen Entfernung zum Objekt.
Von der Beobachtungszeit in UT gelangt man zur heliozentrischen Zeit
durch Addition der heliozentrischen Korrektur 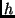 , die sich wie folgt
berechnet:
, die sich wie folgt
berechnet:
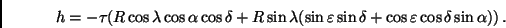 |
(25) |
Hierbei sind 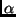 und
und 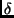 die äquatorialen Koordinaten des Sterns,
die äquatorialen Koordinaten des Sterns,
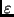 die Schiefe der Ekliptik,
die Schiefe der Ekliptik, 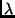 die ekliptikale Länge
der Sonne und
die ekliptikale Länge
der Sonne und 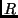 der momentane Radiusvektor Erde-Sonne in Astronomischen
Einheiten. Der Wert für
der momentane Radiusvektor Erde-Sonne in Astronomischen
Einheiten. Der Wert für 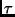 , die Lichtzeit für die astronomische
Längeneinheit, beträgt 0,0057755 Tage.
Die Theorie der Bestimmung der Bahnelemente aus den Eigenschaften
der Lichtkurve wurde von H.N. RUSSEL 1912 [4] entwickelt.
Generell unterscheidet man zwischen direkten und
iterativen Lösungen. Während bei RUSSELs Methode die Elemente unter
bestimmten Annahmen direkt aus den Bestimmungsgleichungen
bestimmt werden, nähert man sich bei der
Methode von WOOD 1969 [5] schrittweise der besten Lösung an.
Bei den modernen Verfahren (z.B. WILSON und DEVINNEY 1971
[6]) werden
alle weiter oben besprochenen Effekte in die Rechnung einbezogen.
Neue Verfahren nutzen auch die Methode der Fourieranalyse für die
Berechnung der Elemente (siehe z.B. GHEDINI 1984 [7]). Eine
moderne
Beschreibung der Theorie der Verfinsterungen bei Bedeckungssternen findet
man z.B. bei KOPAL 1990 [8]. Entwicklungseffekte in
Doppelsternsystemen
sind ausführlich bei KOPAL und RAHE 1982 [9] abgehandelt.
Eine vollständige Analyse der Lichtkurve ist oft schwierig,
rechenzeitintensiv, mit relativ großen Fehlern behaftet
und meistens nur durch den Vergleich mehrerer
Methoden zu erhalten, weil, wie wir weiter oben gesehen haben, die
Form der Lichtkurve dem Einfluß vieler Faktoren unterliegt.
Wir werden deshalb hier das Verfahren der Simulation benutzen, bei der
wir die astrophysikalischen Parameter vorgeben und dann den Einfluß
der Änderung einzelner Parameter auf die Gestalt der Lichtkurve
untersuchen. Für die Simulation steht Ihnen das Programm ALGOL.EXE
zur Verfügung.
, die Lichtzeit für die astronomische
Längeneinheit, beträgt 0,0057755 Tage.
Die Theorie der Bestimmung der Bahnelemente aus den Eigenschaften
der Lichtkurve wurde von H.N. RUSSEL 1912 [4] entwickelt.
Generell unterscheidet man zwischen direkten und
iterativen Lösungen. Während bei RUSSELs Methode die Elemente unter
bestimmten Annahmen direkt aus den Bestimmungsgleichungen
bestimmt werden, nähert man sich bei der
Methode von WOOD 1969 [5] schrittweise der besten Lösung an.
Bei den modernen Verfahren (z.B. WILSON und DEVINNEY 1971
[6]) werden
alle weiter oben besprochenen Effekte in die Rechnung einbezogen.
Neue Verfahren nutzen auch die Methode der Fourieranalyse für die
Berechnung der Elemente (siehe z.B. GHEDINI 1984 [7]). Eine
moderne
Beschreibung der Theorie der Verfinsterungen bei Bedeckungssternen findet
man z.B. bei KOPAL 1990 [8]. Entwicklungseffekte in
Doppelsternsystemen
sind ausführlich bei KOPAL und RAHE 1982 [9] abgehandelt.
Eine vollständige Analyse der Lichtkurve ist oft schwierig,
rechenzeitintensiv, mit relativ großen Fehlern behaftet
und meistens nur durch den Vergleich mehrerer
Methoden zu erhalten, weil, wie wir weiter oben gesehen haben, die
Form der Lichtkurve dem Einfluß vieler Faktoren unterliegt.
Wir werden deshalb hier das Verfahren der Simulation benutzen, bei der
wir die astrophysikalischen Parameter vorgeben und dann den Einfluß
der Änderung einzelner Parameter auf die Gestalt der Lichtkurve
untersuchen. Für die Simulation steht Ihnen das Programm ALGOL.EXE
zur Verfügung.




Next: Versuchsanleitung
Up: Analyse der Beobachtungen
Previous: Spektroskopische Beobachtungen - Die
Contents
Juergen Weiprecht
2002-10-29